Resultats de la cerca
Es mostren 14 resultats
nombre racional
Matemàtiques
Conjunt de fraccions equivalents que representen una mateixa quantitat, entera o no.
Dues fraccions a / b , c / d són equivalents o iguals si, i només si, els parells de nombres enters que les constitueixen compleixen la relació ad = bc Cada classe de fraccions equivalents en aquesta relació d’equivalència és un nombre racional Si la fracció que defineix un nombre racional té numerador múltiple del denominador, és a dir, a = kb k ∈ℤ, la fracció a / b és equivalent a k/ 1, que hom acostuma a escriure en la forma k/ 1 = k En aquest sentit hom pot dir que els nombres enters són un subconjunt dels racionals Entre els nombres racionals hom pot definir les operacions d’addició i…
transposició
Matemàtiques
En una matriu, canvi de les files per les columnes.
Així, la matriu es transforma per transposició en El determinant d’una matriu quadrada és invariant per transposició Una matriu en què la inversa és igual a la transposada, és anomenada ortogonal aquestes matrius representen els moviments lineals que conserven distàncies, angles i productes escalars
Georg Ferdinand Frobenius
Matemàtiques
Matemàtic alemany.
Fou professor a la Universitat de Berlín Investigà en les branques més elevades de l’àlgebra, en connexió amb la teoria de les funcions i dels grups Els nombrosos teoremes que duen el seu nom representen un enriquiment de l’àlgebra clàssica i constitueixen un dels punts de partida de l’àlgebra moderna
suanpan
Matemàtiques
Tipus d’àbac originari de la Xina, on és emprat encara actualment.
Conegut des de temps molt antic, consisteix en un tauler amb una barra transversal que separa dues zones proveïdes d’una sèrie de barretes paralleles amb dues boles a la part de dalt i cinc a la de baix Les boles són desplaçables i tenen un valor de 5 les de la part superior, i d’1 les de la inferior Les distintes columnes representen unitats, desenes, centenes, milers, etc, respectivament Acostant un cert nombre de boles cap a la barra transversal, hom pot representar un nombre decimal qualsevol
metamatemàtica
Matemàtiques
Nom donat per Hilbert a l’estudi del llenguatge format pels enunciats sobre els signes emprats per la matemàtica.
Així, l’enunciat ''tot x més gran que 2 , si és primer és senar’ és un enunciat pròpiament matemàtic, és a dir, un teorema del qual hom pot provar la correcció o la incorrecció a partir d’un determinat conjunt d’axiomes en canvi, són metamatemàtics els enunciats '' x és una variable numèrica’, '' 2 és una constant numèrica’, etc, que caldria que acompanyessin l’enunciat matemàtic anterior per tal de fer-lo comprensible a qui no sabés què representen x i 2 La distinció entre matemàtica i metamatemàtica fou feta per Hilbert a fi d’aconseguir el desenvolupament d’una teoria de la…
teorema de Pitàgores
Matemàtiques
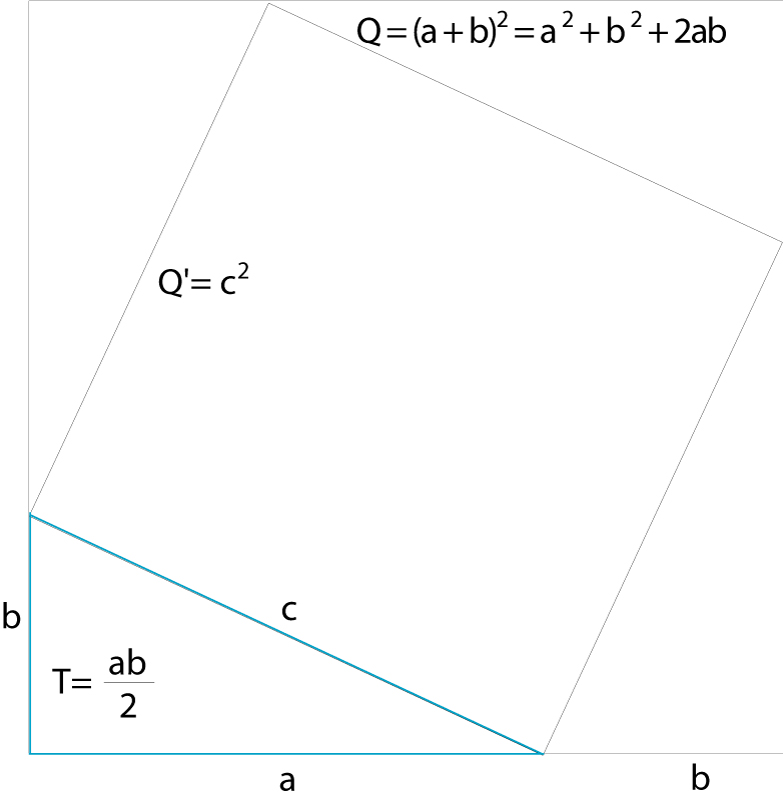
Teorema fonamental de la geometria segons el qual en un triangle rectangle l’àrea del quadrat que té per costat la hipotenusa és igual a la suma de les àrees dels quadrats que tenen per costat els catets.
Si a i b representen les longituds dels catets i c la longitud de la hipotenusa, el teorema Pitàgores és expressat per la igualtat c 2 = a 2 + b 2 Bé que la primera demostració del teorema sembla que fou feta pels membres de l’ escola pitagòrica Pitàgores vers l’any 550 aC, el teorema de Pitàgores, almenys en alguns casos particulars, ja era conegut pel poble egipci vers l’any 2000 aC, pels xinesos vers l’any 1100 aC i pels vedes vers l’any 800 aC D’altra banda, fou a partir del teorema que els pitagòrics descobriren que no n'hi ha prou amb els nombres enters i fraccionaris…
autòmat finit
Matemàtiques
Electrònica i informàtica
Model matemàtic d’un sistema que té un nombre finit d’estats d’entrada i de sortida —els quals representen les diferents configuracions de signes (i estats interns) que representen la capacitat que té el sistema d’enregistrar els esdeveniments passats— i en el qual l’estat de sortida depèn en qualsevol moment de l’entrada present i dels estats interns.
Per tant, un autòmat finit es defineix pel conjunt finit dels estats d’entrada, de sortida i interns possibles per una funció que dóna el següent estat intern corresponent a un estat d’entrada i a un estat intern donats i per una funció que determina l’estat de sortida següent Aquest concepte és essencialment abstracte i té valor tant per a descriure programes com per a descriure aparells Un autòmat finit concret es defineix normalment per mitjà de la seva taula d’estats , que consisteix en una llista de les relacions existents entre els estats d’entrada, els de sortida i els interns Una…
freqüència
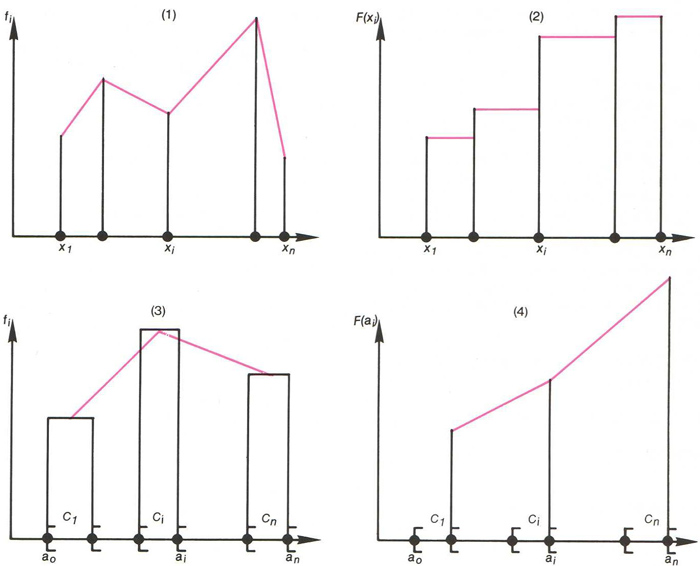
Representacions gràfiques de la freqüència d’una distribució estadística: si el caràcter quantitatiu és discret, (1) és el seu polígon de freqüencies i (2) és la seva corba cumulativa; si el caràcter quantitatiu és continu, (3) és el seu polígon de freqüències i (4) és la seva corba cumulativa
© Fototeca.cat
Matemàtiques
En una distribució estadística d’un caràcter quantitatiu, quocient entre l’efectiu d’un valor concret del caràcter, o d’una classe de valors, i el nombre d’individus que integren la mostra.
Si el caràcter quantitatiu és discret , i pren els valors x 1 ,,x n sobre una mostra de N individus, la freqüència o freqüència relativa del valor x i és el quocient f i = n i / N , on n i és l’ efectiu del valor x i és a dir, el nombre d’individus de la mostra que presenten el valor x i del caràcter La representació gràfica de la funció de distribució x i → f i és una línia poligonal obtinguda en unir els punts de coordenades x i , f i , i =1,, n , anomenada polígon de freqüències Si el caràcter quantitatiu és continu , donada una classe o interval C i = a i - 1 , a i del conjunt de…
relació d’ordre
Matemàtiques
Relació binària R entre els elements d’un conjunt C que és reflexiva, antisimètrica i transitiva.
La parella C, R constitueix un conjunt ordenat És usual la notació ≤per a designar la relació d’ordre desigualtat 5, i a ≤ b és llegit '' a menor o igual a b' , o bé '' a inferior a b' aquesta notació generalitza la coneguda i usual relació “ésser menor que o igual a” que ordena els nombres Unes altres relacions d’ordre importants són la relació d’igualtat, la relació d’inclusió entre conjunts, la relació “ésser divisor de” en els nombres naturals, etc En un conjunt ordenat, són elements notables el màxim , el mínim , el maximal , el minimal , el majorant i el minorant Dos elements…
numeració
Matemàtiques
Art d’expressar tots els nombres amb un conjunt finit de mots i de signes.
El sistema de numeració de l’antic Egipte III millenni aC era decimal , o de base 10, és a dir, hom comptava per unitats, desenes, centenes, etc La unitat, la desena, la centena i el miler eren representats, respectivament, amb els símbols ∣, ⋂, ℮, aquest símbols, fins que la suma de valor dels signes escrits era igual al nombre per exemple, el nombre 1235 era ℮℮⋂⋂⋂∣∣∣∣∣ El sistema de numeració babilònic era de base seixanta i ja utilitzava una notació posicional, cosa que suposa la introducció del zero Era, doncs, un sistema essencialment semblant a l’actual, bé que confusionari, puix que,…