Resultats de la cerca
Es mostren 6 resultats
cardioide
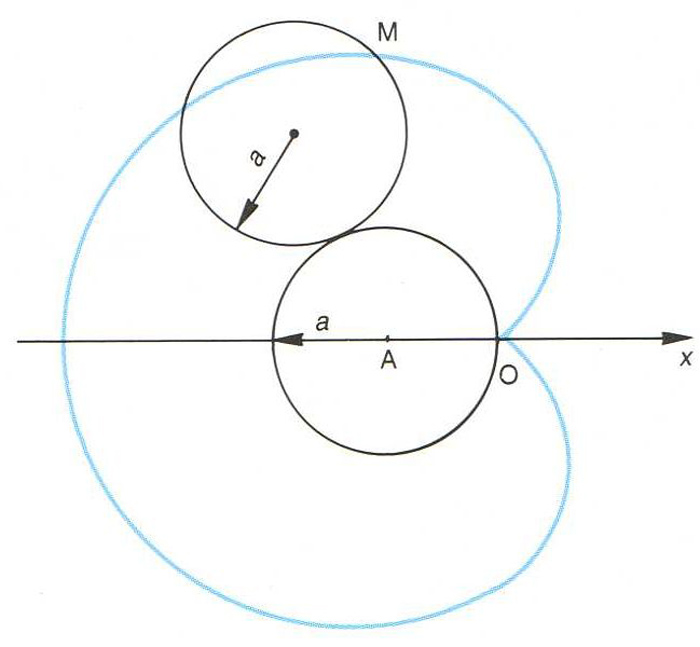
Cardioide determinada pel punt fix M d’un cercle de radi a que roda sense lliscar sobre un cercle fix de radi a i centre A. O és el punt de retrocés
© fototeca.cat
Matemàtiques
Epicicloide singular engendrada per les posicions d’un punt d’un cercle de radi a que roda sense lliscar per damunt d’un altre cercle del mateix radi.
Té un punt de retrocés O , respecte al qual l’equació de la cardioide en coordenades polars és ρ = 2 a 1-cos θ La longitud de la cardioide és aleshores 16 a i l’àrea és 6π a 2
trocoide
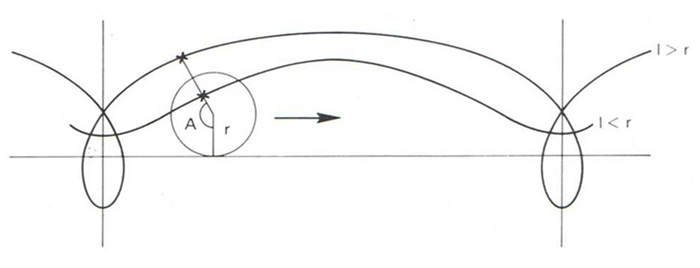
Trociode
© fototeca.cat
Matemàtiques
Corba descrita per un punt fixat a un cercle quan aquest cercle roda sense lliscament sobre una línia recta fixa.
Si el radi del cercle és r , la distància del punt generador al centre del cercle és l i A és l’angle determinat pel punt quan el cercle ha rodat A radiants, aleshores les equacions paramètriques de la trocoide són x = rA-l sin A y = r-l cos A Si l és major que r punt exterior al cercle, la trocoide descriu rulls si l és menor que r punt interior al cercle, la trocoide no toca mai la línia recta fixa base del desplaçament si el punt és el centre del cercle, la trocoide és una recta si l és igual a r punt de la circumferència, la trocoide és aleshores una cicloide
deltoide
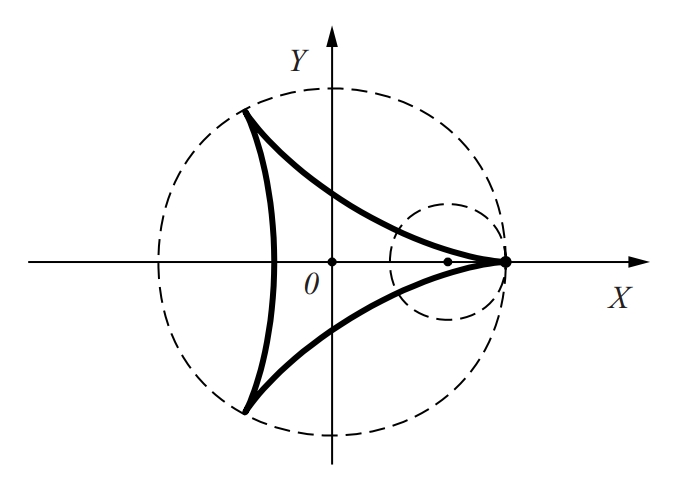
deltoide
Matemàtiques
Hipocicloide d’un cercle de radi k que roda, sense lliscar, dintre d’un altre que té el radi triple.
Les seves equacions paramètriques són x = k 2cos t + cos 2t , i y = k 2sin t + sin 2 t
epicicloide
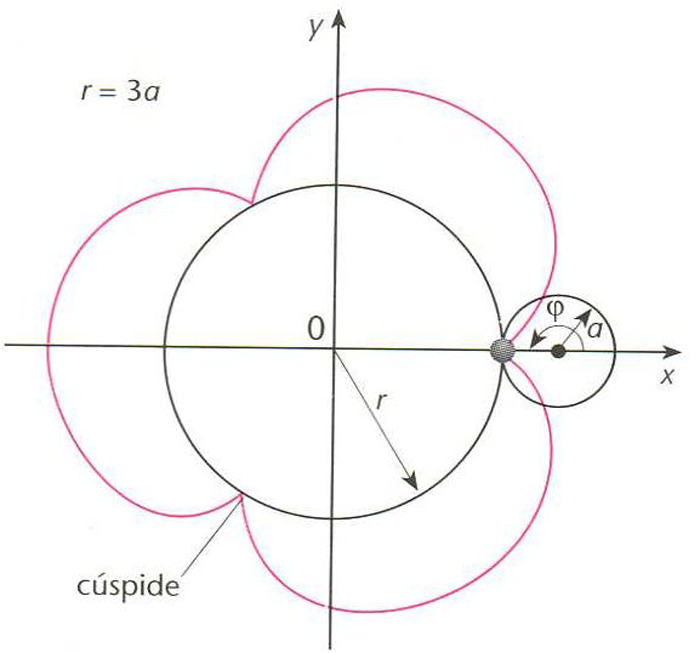
Epiciloide
© fototeca.cat
Matemàtiques
Corba descrita per un punt d’una circumferència que roda sense lliscar sobre una altra, mantenint-se tangents exteriorment ( cicloide
).
La seva equació és on r és el radi de la circumferència fixa, i a , el radi de la circumferència mòbil Si r = na , l’epicidoide té n cúspides n , nombre natural Si r = a la corba degenera en una cardioide Si r= 2 a , ho fa en una nefroide
polhòdia
Física
Matemàtiques
Corba que descriu sobre l’el·lipsoide el punt de contacte d’un el·lipsoide d’inèrcia amb el pla en què aquest roda.
Geomètricament, és definida pels punts de l’ellipsoide en què el pla tangent equidista del centre de l’ellipsoide El pol terrestre descriu una polhòdia sobre la superfície del planeta, a causa del moviment de precessió de l’eix de rotació de la Terra al voltant de l’eix d’inèrcia
hipocicloide
Matemàtiques
Corba engendrada per un punt fix d’una circumferència que roda, sense lliscar, per dins d’una altra, mantenint-se ambdues tangents interiors.
La seva equació és on r és el radi de la circumferència fixa, i a , el radi de la circumferència mòbil L’equació s’obté, doncs, de la de l'epicicloide fen a negativa Quan r= 3 a és una deltoide i quan r= 4 a és una astroide