Resultats de la cerca
Es mostren 87 resultats
sèrie
Matemàtiques
Suma indicada d’un conjunt finit o infinit ordenat de termes.
La teoria de sèries s’ocupa especialment del cas infinit numerable Així, una sèrie és donada per una successió de nombres a₁ , a₂ , , a n , on a n és dit terme general n -èsim de la successió i una successió associada formada per les sumes parcials a₁ , a₁ + a₂ , a₁ + a₂ + a₃ , , a₁ + + a n , Simbòlicament hom representa una sèrie per , o bé a₁ + a₂ + a n + Si la successió de sumes parcials és convergent cap a un límit S , hom diu que la sèrie és convergent i de suma S En cas de no existir aquest límit, la sèrie és dita divergent Una sèrie és dita positiva o negativa segons que tots…
sèrie alternada
Matemàtiques
Sèrie els termes de la qual són alternativament positius i negatius ( sèrie).
sèrie trigonomètrica
Matemàtiques
Cadascuna de les sèries de funcions Σfi , amb fi (x) = an cos nx + bn sin nx
.
Hom demostra que si una sèrie trigonomètrica convergeix uniformement per a x ∈ -π,π la funció f cap a la qual convergeix és contínua i periòdica amb període 2π, i que els coeficients a n , b n s’hi relacionen
desenvolupament en sèrie
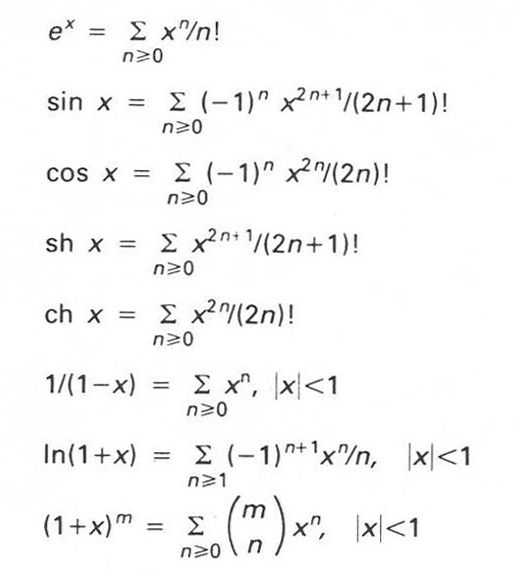
Desenvolupament en sèrie de potències d’algunes funcions
©
Matemàtiques
Expressió d’una funció real, de variable real o complexa,
f(x) ∞
, en termes d’una sèrie de funcions
:
.
La legitimitat d’aquesta igualtat depèn de la convergència de la successió de sumes parcials, en el domini de definició de fx Hom empra, generalment, el desenvolupament en sèrie de potències o sèrie entera, que resulta del teorema de Taylor , i, en el cas de funcions periòdiques, hom empra el desenvolupament en sèrie de Fourier anàlisi de Fourier
sèrie de potències
Matemàtiques
Donada una funció real de variable real f (x) derivable indefinidament en el punt x0, sèrie Σ an (x-x0)n amb an = (1/ n !) fn (x0).
Es compleix que f x = Σ a n x- x 0 n per a tots els punts x tals que | x- x 0 | < R, on R és el radi de convergència de la sèrie Aquesta sèrie és anomenada sèrie que desenvolupa la funció f en un entorn del punt x 0 , o sèrie de Taylor de f en el punt x 0 La sèrie de potències és utilitzada per a expressar el desenvolupament en sèrie d’una funció Així, per exemple, hom té la sèrie exponencial , que és convergent per a tot x
sèrie de Renard
Matemàtiques
Sèrie formada pels termes d’una progressió geomètrica compresos entre 1 i 10, la raó de la qual és
, n essent, generalment, 5, 10, 20 o 40.
La més corrent és l’obtinguda amb n = 10, amb la qual cosa la raó val =1,26 Els termes d’aquesta sèrie són 1 1,25 1,6 2 2,5 3,15 4,5 6,3 8 10 Aquesta sèrie, ideada el 1879 per l’enginyer Charles Renard Damblaim 1847 — Meudon 1905, té aplicació en diversos camps industrials
sèrie de funcions
Matemàtiques
Successió de funcions {
F n
} amb
, on les
f i
són també funcions.
Hom la indica per Σ f n Si { F n } té per límit una funció f , hom diu que la sèrie Σ f n és convergent cap a la funció f i que f és la seva suma, dins el domini on això tingui sentit Si les f i són funcions potencials, f i x = a i x i , la sèrie Σ f n és anomenada sèrie de potències Si la variable x és complexa hom pot demostrar que hi ha un nombre positiu R tal que per a tot x tal que | x | < R la sèrie numèrica Σ a n x n és absolutament convergent, mentre que per a tot x tal que | x | > R la sèrie numèrica Σ a n x n…
majorar una successió
Matemàtiques
Substituir els seus termes per uns altres de més grans (criteri emprat a vegades per a estudiar el caràcter de convergència de la successió o sèrie).
harmònic
Física
Matemàtiques
Cadascun dels termes de la sèrie de Fourier d’una funció periòdica (anàlisi de Fourier).
El terme de la sèrie de freqüència més baixa és anomenat harmònic fonamental o primer harmònic , i els altres termes són anomenats harmònics del fonamental
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- Pàgina següent
- Última pàgina