Resultats de la cerca
Es mostren 274 resultats
superfície desenvolupable
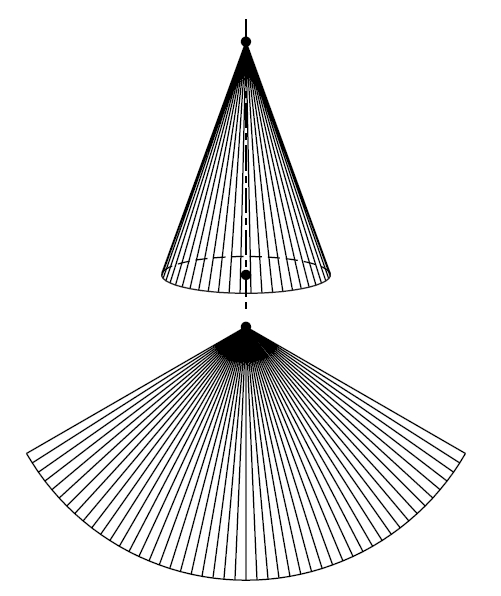
Superfície desenvolupable i el seu desenvolupament
Matemàtiques
Superfície isomètrica al pla, és a dir, que hom pot desplegar sense deformació sobre un pla.
Perquè una superfície sigui desenvolupable cal que contingui rectes superfície reglada i que el vector normal a la superfície sigui constant al llarg de cada recta En són exemples els cons, els cilindres i les superfícies constituïdes per totes les tangents a una corba en l’espai Qualsevol superfície desenvolupable és d’un d’aquests tres tipus citats
angle dièdric
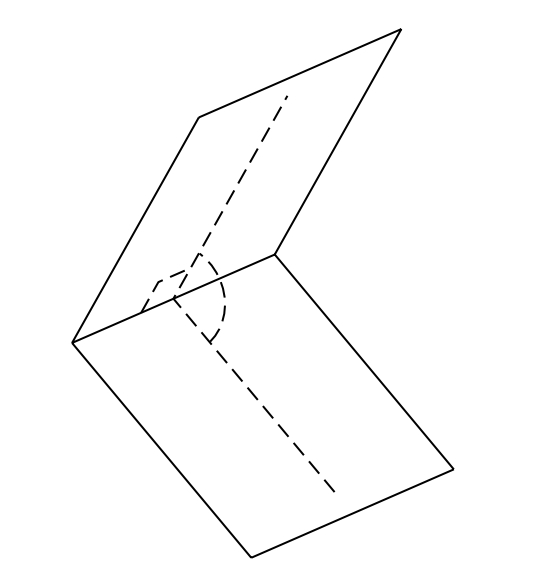
Anglè dièdric i el seu angle rectilini
© Fototeca.cat
Matemàtiques
Regió de l’espai compresa entre dos semiplans que tenen la mateixa recta (anomenada aresta de l’angle dièdric) com a vora.
Es mesura per l’angle rectilini corresponent al diedre associat
Pitàgores
Filosofia
Matemàtiques
Filòsof i matemàtic grec, fundador de l’escola o secta politicoreligiosa que porta el seu nom.
Malgrat la incertesa de les notícies que hom en té, sembla que s’establí, procedent de l’Àsia Menor, a Crotona ~530 aC, on fundà una comunitat ascètica centrada en l’estudi de les matemàtiques i activa en els afers polítics de la ciutat, i d’on, ja vell, hagué de fugir a la veïna Metapont arran d’una rebellió que hi tingué lloc La saviesa del mestre no fou divulgada pels seus deixebles, tal com establien els preceptes de la comunitat, motiu pel qual és difícil de destriar la part de les creences del pitagorisme que correspon a Pitàgores mateix i no a aportacions dels seus deixebles Sembla,…
hessià | hessiana
Matemàtiques
Dit de la matriu o del seu determinant formats per les derivades de segon ordre d’una funció de diverses variables.
Per exemple, la hessiana de f x , y = x 2 - 2 xy 2 és L’estudi dels valors de la matriu hessiana és important en la determinació de punts singulars i extrems de funcions de diverses variables Rep el seu nom del matemàtic LO Hesse
tor
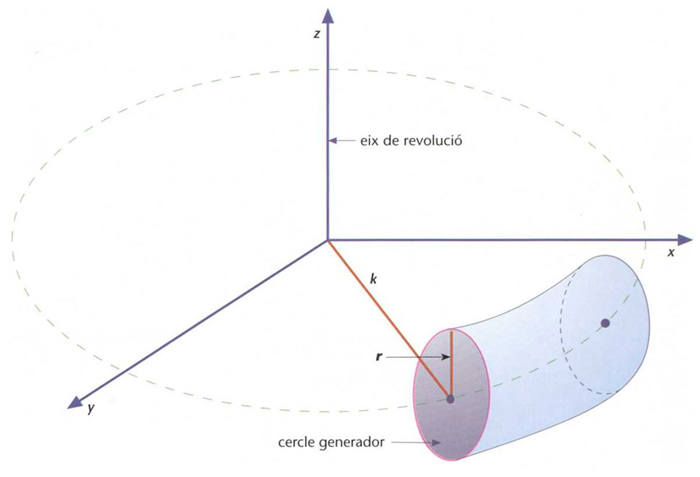
Generació d’un tor per un cercle
© Fototeca.cat
Matemàtiques
Superfície generada per la rotació, en l’espai, d’un cercle al voltant d’un eix del seu pla que no talla el cercle.
És la forma d’un anell de contorn circular i rodó Si r és el valor del radi del cercle generador, k la distància del centre a l’eix de revolució eix z , l’equació del tor és el seu volum val 2π kr, i l’àrea de la seva superfície, 4 π 2 kr
freqüència
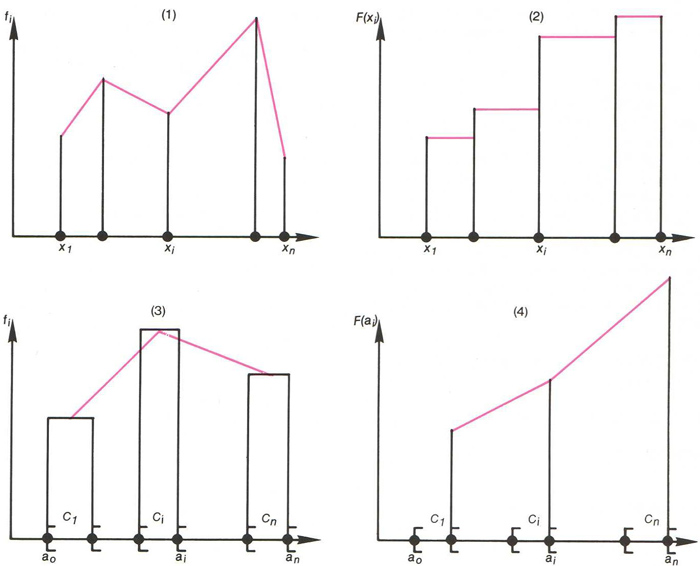
Representacions gràfiques de la freqüència d’una distribució estadística: si el caràcter quantitatiu és discret, (1) és el seu polígon de freqüencies i (2) és la seva corba cumulativa; si el caràcter quantitatiu és continu, (3) és el seu polígon de freqüències i (4) és la seva corba cumulativa
© Fototeca.cat
Matemàtiques
En una distribució estadística d’un caràcter quantitatiu, quocient entre l’efectiu d’un valor concret del caràcter, o d’una classe de valors, i el nombre d’individus que integren la mostra.
Si el caràcter quantitatiu és discret , i pren els valors x 1 ,,x n sobre una mostra de N individus, la freqüència o freqüència relativa del valor x i és el quocient f i = n i / N , on n i és l’ efectiu del valor x i és a dir, el nombre d’individus de la mostra que presenten el valor x i del caràcter La representació gràfica de la funció de distribució x i → f i és una línia poligonal obtinguda en unir els punts de coordenades x i , f i , i =1,, n , anomenada polígon de freqüències Si el caràcter quantitatiu és continu , donada una classe o interval C i = a i - 1 , a i del conjunt de…
tancat | tancada
integral impròpia
Matemàtiques
Integral que, a causa de no ésser definida o fitada, la funció a integrar, en algun punt del seu domini de definició, no és calculable directament.
Així, quan la funció f no és definida o fitada a un punt c del seu domini de definició a,b , hom defineix la integral impròpia de f en a,b per si aquests dos límits existeixen, la integral és anomenada convergent i, en cas contrari, divergent Un altre cas d’integral impròpia s’esdevé quan un dels límits d’integració és infinit la integral és definida aleshores, segons el cas, per Les integrals impròpies són també anomenades integrals generalitzades
frontera
Matemàtiques
Conjunt de punts que separa l’interior d’una regió del seu exterior, de manera que qualsevol entorn d’un punt de la frontera té punts de l’interior i de l’exterior.
Topològicament, la frontera d’una part A d’un espai topològic és la intersecció de l’adherència de A amb l’adherència del seu complementari
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina