Resultats de la cerca
Es mostren 387 resultats
freqüència
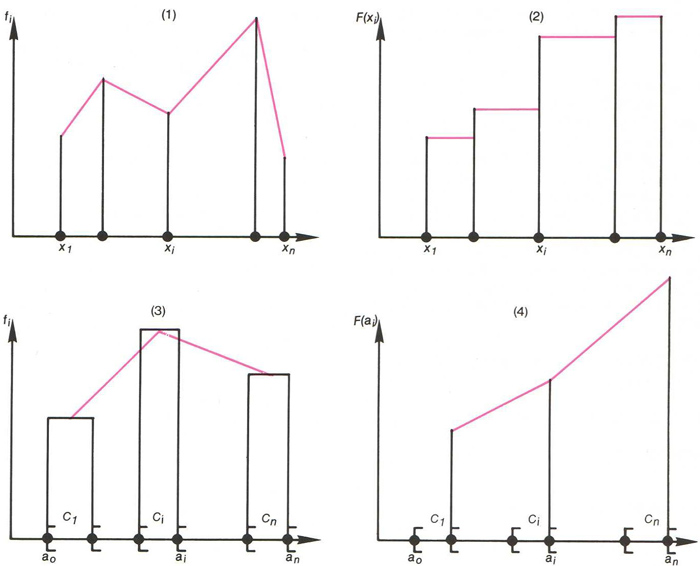
Representacions gràfiques de la freqüència d’una distribució estadística: si el caràcter quantitatiu és discret, (1) és el seu polígon de freqüencies i (2) és la seva corba cumulativa; si el caràcter quantitatiu és continu, (3) és el seu polígon de freqüències i (4) és la seva corba cumulativa
© Fototeca.cat
Matemàtiques
En una distribució estadística d’un caràcter quantitatiu, quocient entre l’efectiu d’un valor concret del caràcter, o d’una classe de valors, i el nombre d’individus que integren la mostra.
Si el caràcter quantitatiu és discret , i pren els valors x 1 ,,x n sobre una mostra de N individus, la freqüència o freqüència relativa del valor x i és el quocient f i = n i / N , on n i és l’ efectiu del valor x i és a dir, el nombre d’individus de la mostra que presenten el valor x i del caràcter La representació gràfica de la funció de distribució x i → f i és una línia poligonal obtinguda en unir els punts de coordenades x i , f i , i =1,, n , anomenada polígon de freqüències Si el caràcter quantitatiu és continu , donada una classe o interval C i = a i - 1 , a i del conjunt de…
element mínim
Matemàtiques
En un conjunt ordenat (X,≤), element x si, i només si, per a tot altre element y ∈ X, x ≤ y
.
L’element mínim d’un conjunt, si existeix, és únic
element màxim
Matemàtiques
En un conjunt ordenat (X,≤) element x si, i només si, per a tot altre element y ∈ X, y ≤ x
.
L’element màxim d’un conjunt, si existeix, és únic
element adherent
Matemàtiques
En un espai topològic OOOX,OOOooo, un element x ∈ X és adherent a un conjunt A ⊆ X si, i només si, tot entorn obert d’x talla a A
.
El conjunt de tots els punts adherents a A rep el nom d’adherència o clausura d' A i és designat Ā i es designat Ā i, a voltes, CL A És el més petit conjunt tancat que conté el conjunt A Un conjunt A és tancat per a la topologia OOO si, i només si, Ā =
enter
Matemàtiques
Classe d’equivalència que la relació (a,b)R(c,d), si, i només si, a+d = b+c, indueix en el conjunt producte ℕ × ℕ (ℕ essent el conjunt dels nombres naturals).
El conjunt d’aquestes classes d’equivalència conjunt quocient és el conjunt dels nombres enters ℤ = {0, ±1, ±2, ±3, } Hom anomena representant canònic d’un enter a,b aquell en què o a o b és 0 Si l’esmentat representant canònic és de la forma m, 0, aquest és un enter positiu , representat també per + m si és la forma 0, m , es tracta d’un enter negatiu , habitualment representat per - m i si és 0,0, és l' enter nul , o sigui 0 En el conjunt ℤ hom defineix dues operacions la suma és definida per a, b + c, d = a + c , b + d , i el producte , per a, b c, d = ac + bd, ad + bc Tal…
rosa
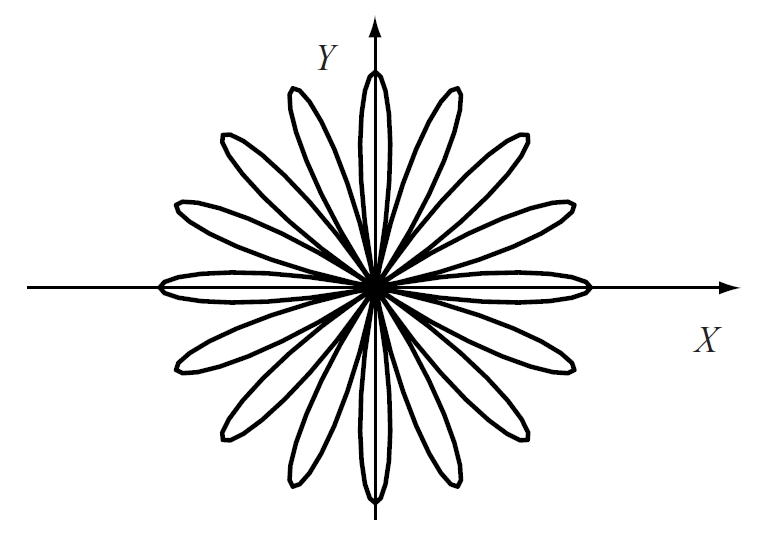
rosa
Matemàtiques
Corba plana algebraica que és la corba pedal d’una epicicloide respecte del centre, d’equació polar r = k cos (ma), de manera que, si m és un nombre enter senar, hi ha m pètals i, si m és parell, hi ha 2m pètals.
Si m = 3, es parla del trifoli si m = 2, és un quadrifoli, i si m = 1 ⁄ 3, és la corba pedal d’una cardioide
inclusió
Matemàtiques
Relació d’ordre parcial entre conjunts, notada mitjançant el símbol ⊂(o, a vegades, ⊆), definida per la condició A⊂B (o A⊆B) si i només si tots els elements de A pertanyen a B
.
En aquest cas, hom diu que el conjunt A és inclòs en el conjunt B o que A és un subconjunt de B Si A no és inclòs en B , hom ho denota per A ⊄ B
ssi
Matemàtiques
Abreviatura de ‘‘si i només si’’, especialment en lògica matemàtica.
antilogaritme
Matemàtiques
Nombre del qual és logaritme un nombre donat; si a és el logaritme de b, b és l’antilogaritme de a.
Busca l’antilogaritme és el procés invers de buscar el logaritme Si a és el logaritme de b, b és l’antilogaritme de a S’usen sovint els símbols antilog x , aln x , exp x , etc
regla de Ruffini
Matemàtiques
Mètode per a comprovar, donats un polinomi p(x) i un valor a, si aquest valor és solució de l’equació p(x) = 0, és a dir, si x - a divideix el polinomi p(x).
El mètode dóna, a més, el polinomi p x / x-a , i així, d’una forma successiva, hom pot arribar per reiteració a determinar totes les solucions reals del polinomi És, però, un mètode de comprovació i no pas un algorisme de resolució El mètode és el següent sigui, per exemple, el polinomi x 2 + x - 2 hom escriu els coeficients 1, 1, -2, i a continuació, suposat un valor qualsevol escollit entre els divisors del coeficient independent que en aquest cas és -2, per exemple 1, hom fa els càlculs següents És a dir, el primer coeficient resta igual al segon hom suma el producte del primer coeficient…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina