Resultats de la cerca
Es mostren 22 resultats
Nicolas Bourbaki
Matemàtiques
Pseudònim col·lectiu d’un grup de matemàtics francesos, antics alumnes de l’École Normale Supérieure.
El 1930 començà a aparèixer aquesta signatura en els Comptes Rendus de l’Académie Française des Sciences, i a partir del 1939 iniciaren la publicació dels cèlebres Éléments de Mathématiques Adscrits a l’escola formalista formalisme , han exercit una gran influència en la matemàtica actual l’elaboració dels Éléments sembla ésser una realització del programa de David Hilbert Bé que el funcionament intern i el nom dels membres del grup Bourbaki han estat mantinguts en secret, hom creu que els fundadors foren Henri Cartan, Claude Chevalley, Samuel Eilenberg, Jean Dieudonné i André Weil, entre d…
aràbic | aràbiga
Matemàtiques
Dit dels signes gràfics del sistema de numeració posicional i decimal utilitzats als països occidentals actualment (numeració, xifra).
Sembla que aquests signes eren d’origen indi i foren el model de les xifres dels àrabs occidentals, més semblants a les índies que no pas les dels àrabs orientals Sembla cert que, a través de Còrdova, foren conegudes a Catalunya a la segona meitat del segle X Consta que Gerbert el futur papa Silvestre II les aprengué durant la seva estada a Vic, Girona i Barcelona, entre el 967 i el 970 Les figuracions més antigues conegudes entre els llatins són les dels còdexs Albeldense i Emilianense ara a El Escorial, escrits el 976 i el 994 respectivament Només consten de nou xifres en ordre invers, és a…
Pitàgores
Filosofia
Matemàtiques
Filòsof i matemàtic grec, fundador de l’escola o secta politicoreligiosa que porta el seu nom.
Malgrat la incertesa de les notícies que hom en té, sembla que s’establí, procedent de l’Àsia Menor, a Crotona ~530 aC, on fundà una comunitat ascètica centrada en l’estudi de les matemàtiques i activa en els afers polítics de la ciutat, i d’on, ja vell, hagué de fugir a la veïna Metapont arran d’una rebellió que hi tingué lloc La saviesa del mestre no fou divulgada pels seus deixebles, tal com establien els preceptes de la comunitat, motiu pel qual és difícil de destriar la part de les creences del pitagorisme que correspon a Pitàgores mateix i no a aportacions dels seus deixebles Sembla,…
Bhāskara
Astronomia
Matemàtiques
Matemàtic i astrònom indi anomenat, també, Ācārya, «el savi».
Fou un dels més genials matemàtics indis i, a part altres treballs matemàtics i astrònomics, introduí el concepte d’infinit en matemàtiques, ja substituïa les incògnites per lletres i sembla que intuí els productes entre signes El seu llibre més famós és el Siddhānta-śiromani ‘Fi del sistema’, 1150, dividit en dues parts sobre matemàtiques i dues sobre astronomia
Lewis Carroll
Literatura anglesa
Matemàtiques
Pseudònim del matemàtic i escriptor anglès Charles Lutwidge Dodgson.
Professor de matemàtiques a Oxford, publicà moltes obres científiques Escriví narracions pseudoinfantils que, tot i que la matèria narrativa sembla abocada a l’absurd, són susceptibles d’interpretació La seva obra més coneguda és Alícia al país de les meravelles 1865 Altres contes seus són Through the looking-glass ‘A través del mirall’, 1872, Sylvie and Bruno 1889, The Hunting of the Snark ‘La cacera del Snark’, 1876
postulat d’Euclides
Matemàtiques
Postulat cinquè del sistema de postulats d’Euclides, que, en llenguatge modern, diu que, donada una recta i un punt exterior, hom només pot traçar per aquest una recta paral·lela a la recta donada.
Aquesta proposició, enunciada per Euclides com a postulat, semblà als geòmetres posteriors que era demostrable a partir dels altres postulats del sistema, és a dir, que era un teorema Fins al s XIX se succeïren els intents de demostració sense resultat, fins que gairebé simultàniament Gauss, Bolyai i Lobačevskij tractaren de desenvolupar una teoria basada en els altres postulats d’Euclides i la negació del cinquè Si aquest hagués estat un teorema, la seva negació hauria conduït a una contradicció no tan sols no trobaren cap contradicció, sinó que obtingueren noves geometries, per…
teorema de Pitàgores
Matemàtiques
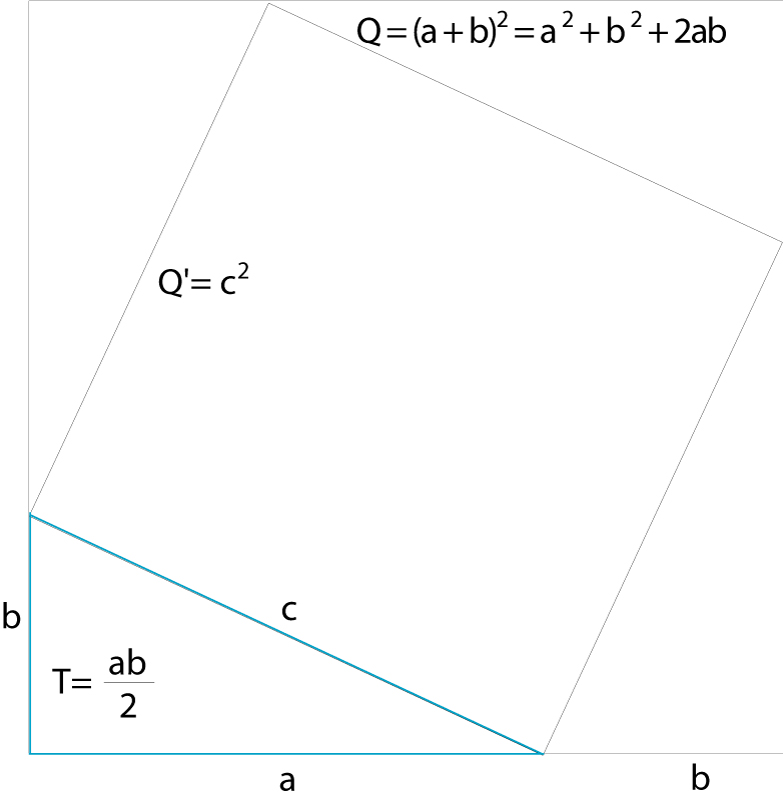
Teorema fonamental de la geometria segons el qual en un triangle rectangle l’àrea del quadrat que té per costat la hipotenusa és igual a la suma de les àrees dels quadrats que tenen per costat els catets.
Si a i b representen les longituds dels catets i c la longitud de la hipotenusa, el teorema Pitàgores és expressat per la igualtat c 2 = a 2 + b 2 Bé que la primera demostració del teorema sembla que fou feta pels membres de l’ escola pitagòrica Pitàgores vers l’any 550 aC, el teorema de Pitàgores, almenys en alguns casos particulars, ja era conegut pel poble egipci vers l’any 2000 aC, pels xinesos vers l’any 1100 aC i pels vedes vers l’any 800 aC D’altra banda, fou a partir del teorema que els pitagòrics descobriren que no n'hi ha prou amb els nombres enters i fraccionaris per a mesurar…
programació matemàtica
Matemàtiques
Conjunt de procediments matemàtics per a resoldre problemes d’òptims condicionats, és a dir, problemes consistents a maximitzar o minimitzar una funció numèrica de diverses variables subjectes a certes limitacions.
Comprèn la programació lineal i les seves aplicacions transport, paramètrica, estocàstica, de nombres enters, la programació quadràtica denominada d’acord amb el grau de les equacions que cal optimitzar i la programació dinàmica , que es refereix més a la técnica computacional que no pas a un tipus particular de problema no lineal Aquestes tècniques tenen un origen recent Sembla que la programació lineal fou emprada per Monge, el 1776, però no fou coneguda fins el 1939, que l’economista soviètic LVKantorovič la descobrí La situació política impedí el desenvolupament i la difusió d’aquesta…
espai topològic
Matemàtiques
Conjunt X en el qual s’ha donat una topologia
.
Els conjunts de la família donada són anomenats oberts , i llurs complementaris, tancats Rep el nom d' entorn obert d’un punt tot conjunt obert que el conté Base de l’espai topològic és una família de conjunts oberts que per reunió poden donar qualsevol altre obert Alguns espais topològics tenen llur topologia definida per mitjà d’una distància, la qual determina la base d’oberts de la topologia formada per les boles o esferes En són exemples la recta real ℝ i els espais euclidians de dimensions superiors ℝ n Un subespai d’un espai topològic és una part de l’espai amb la topologia induïda…
Benet Baïls
Filosofia
Història
Matemàtiques
Matemàtic i erudit il·lustrat.
Inicià la seva formació científica i humanística a Tolosa de Llenguadoc —on sembla que no acabà els estudis de teologia— i la completà a París, on exercí el càrrec de secretari de l’ambaixador d’Espanya Posteriorment residí a Madrid fins a la seva mort Després dels seus primers treballs, publicats en francès, i de collaboracions posteriors en obres collectives en la mateixa llengua, es distingí per la seva tasca de difusió de la cultura científica a la península Ibèrica, on les seves obres foren adoptades com a llibres de text pels collegis i les universitats, especialment els Elementos de…