Resultats de la cerca
Es mostren 27 resultats
simulació
Matemàtiques
Tècnica emprada en investigació operativa.
Consisteix a construir un model simbòlic d’un sistema o d’un procés complex, de manera que els seus elements siguin representats mitjançant els processos lògics i aritmètics que hom pot executar amb un programa d’ordinador, a fi d’estudiar el comportament del sistema i mesurar-ne les propietats dinàmiques, a base d’obtenir les característiques estadístiques del dit comportament Això permet d’avaluar i comparar diferents estratègies d’operació del sistema, sense que aquest existeixi realment Les aplicacions més conegudes d’aquesta tècnica han estat fetes en l’estudi de xarxes d’…
godelització
Matemàtiques
Tècnica introduïda per Kurt Gödel l’any 1931 que consisteix a reduir a nombres naturals les paraules i frases d’un cert llenguatge.
Si hom disposa d’un cert llenguatge L = { a 1 ,, a n } i a cada símbol a i li associa un cert nombre senar g a i per exemple, g a i = 2 i + 1 i, a cada paraula , on cada és una de les lletres a j ∈ L , el nombre , on p r és el r -èsim nombre primer Ara hom pot estendre aquesta tècnica a frases, on cada OOO és una de les lletres
ortografia
Disseny i arts gràfiques
Matemàtiques
Tècnica de la geometria projectiva consistent a fer projeccions ortogonals en un pla vertical.
programació matemàtica
Matemàtiques
Conjunt de procediments matemàtics per a resoldre problemes d’òptims condicionats, és a dir, problemes consistents a maximitzar o minimitzar una funció numèrica de diverses variables subjectes a certes limitacions.
Comprèn la programació lineal i les seves aplicacions transport, paramètrica, estocàstica, de nombres enters, la programació quadràtica denominada d’acord amb el grau de les equacions que cal optimitzar i la programació dinàmica , que es refereix més a la técnica computacional que no pas a un tipus particular de problema no lineal Aquestes tècniques tenen un origen recent Sembla que la programació lineal fou emprada per Monge, el 1776, però no fou coneguda fins el 1939, que l’economista soviètic LVKantorovič la descobrí La situació política impedí el desenvolupament i la difusió d’aquesta…
càlcul diferencial
Matemàtiques
Part de l’anàlisi matemàtica, i, més concretament, de l’anàlisi infinitesimal, que tracta de totes les qüestions relacionades amb els conceptes fonamentals de derivada (ordinària o parcial) i de diferencial d’una funció.
Hom el considera com una teoria conceptual estesa també com a tècnica de càlcul que permet de traduir les propietats geomètriques i físiques de l’espai en forma analítica, independentment del sistema de coordenades concret al qual hom ha referit l’espai
Emanuel Lasker
Escacs
Matemàtiques
Jugador d’escacs i matemàtic alemany d’origen jueu.
Es proclamà campió del món el 1894 en vèncer Wilhelm Steinitz, títol que conservà fins el 1921 La seva tècnica es distingí pel caràcter eminentment posicional, continuador del de Steinitz, i donà una embranzida definitiva a la nova concepció del joc d’escacs
operació lògica
Matemàtiques
Operació no aritmètica que permet d’obtenir, a partir d’una o més variables booleanes, una altra variable booleana.
Són particularment importants les cinc operacions lògiques fonamentals la negació o complement operació NO la intersecció, conjunció o producte lògic operació I la reunió, unió o suma lògica operació O, dita també O inclusiu l' exclusió o conjunció inversa operació NI en anglès NOR i la incompatibilitat o reunió inversa operació ON en anglès NAND És emprada també com a operació auxiliar l’operació dilema , anomenada també O exclusiu Les operacions lògiques constitueixen la base tècnica de la lògica electrònica i són emprades en el càlcul dels circuits automàtics combinatoris i…
mètode dels elements finits
Matemàtiques
Mètode numèric per a resoldre problemes d’equacions diferencials en derivades parcials.
Matemàticament és una extensió de la tècnica de Rayleigh-Ritz-Galerkin el problema es planteja en forma variacional i hom aproxima la solució mitjançant una combinació lineal de funcions senzilles, en aquest cas funcions polinòmiques a trossos, nulles excepte en un petit domini dintre del qual són polinomis de grau baix El mètode aparegué els anys seixanta entorn de l’aplicació dels ordinadors als càlculs elàstics d’estructures, superà molt de pressa els mètodes de diferències finites i amplià ràpidament el seu camp d’aplicacions i es mostrà molt potent especialment quan la…
mètode dels mínims quadrats
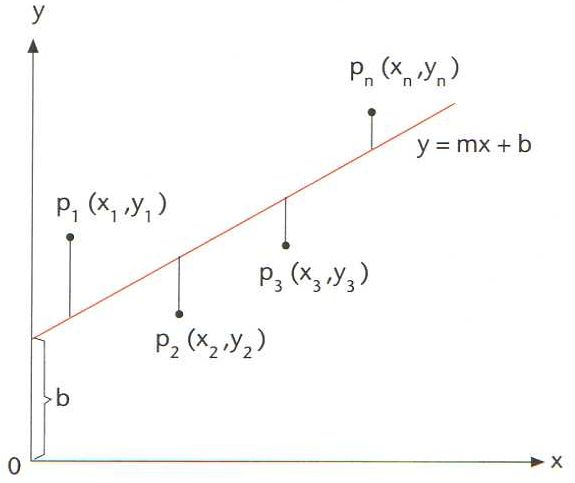
Representació de la recta y=mx + b obtinguda pel mètode dels mínims quadrats
© Fototeca.cat
Matemàtiques
Donat un conjunt de n punts del pla (x1, y1), (x2, y2), ... (xn, yn), mètode que permet de trobar l’equació y = mx + b de la recta que compleix la condició d’ésser la que més s’apropa als punts donats.
Hom defineix matemàticament la dita condició exigint que la suma dels quadrats de les desviacions, ha d’ésser mínima, entenent per desviació en un punt x i , y i la diferència d i = y i - mx i + b Hom pot demostrar que aquella condició condueix a les dues equacions a partir de les quals hom pot calcular els coeficients m i b de la recta, la qual és anomenada també recta de regressió D’altra banda, el mètode dels mínims quadrats serveix també per a ajustar funcions més complexes que la d’una recta, tals com funcions polinòmiques, exponencials, etc, i és utilitzat en l’estudi de la…
Emmanuel Candès
Matemàtiques
Matemàtic francès.
Graduat en enginyeria per l’École Polytechnique de París 1993, obtingué el doctorat en estadística a la Universitat de Stanford Estats Units l’any 1998, on s’incorporà com a professor assistent fins el 2000 Aquest any passà al California Institute of Technology, d’on el 2006 ocupà la càtedra Ronald and Maxine Linde de matemàtiques aplicades i computacionals L’any 2009 retornà a Stanford Es important la seva contribució a l’estudi de les ondetes, que repercutí posteriorment en el camp de la compressió de dades , en el qual amb Terence Tao desenvolupà la teoria del compressed sensing 2006, que…