Resultats de la cerca
Es mostren 13 resultats
asímptota
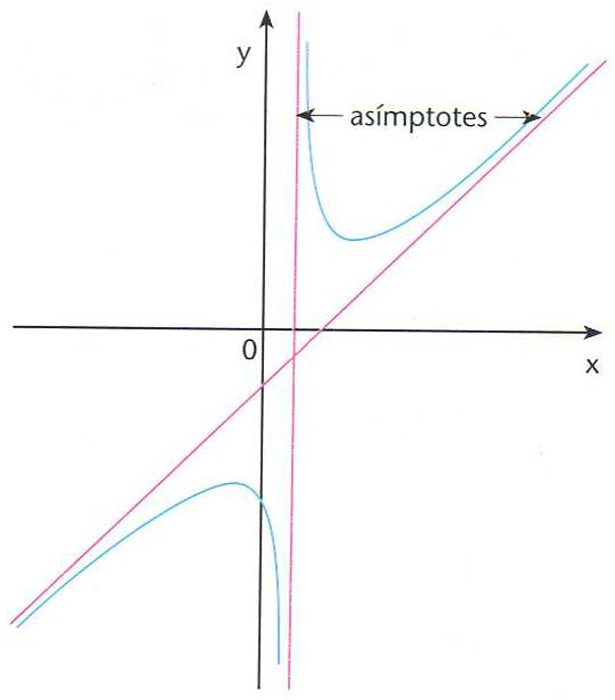
Asímptotes
Matemàtiques
Recta a la qual s’acosta un punt variable sobre una branca de corba quan el punt s’allunya cap a l’infinit.
Per a poder afirmar que una branca de corba té una asímptota cal que, si el punt P es mou sobre aquesta de manera que la distància de P a l’origen de coordenades O creix infinitament, la direcció de la recta OP tingui un límit determinat Hom troba aquest límit per mitjà del quocient y/x = tg a Coneguda la direcció de l’asímptota, hom determina la seva ordenada a l’origen per la condició que la distància entre dos punts que tinguin igual abscissa, un sobre la corba, l’altre sobre l’asímptota, tingui límit zero quan aquella abscissa comuna es fa infinita Així, per exemple, la hipèrbola té dues…
normalització
Matemàtiques
Canvi d’escala que fa que una suma o una integral tingui un valor unitat.
La normalització és assolida, generalment, mitjançant l’ajust d’una constant arbitrària
element de superfície
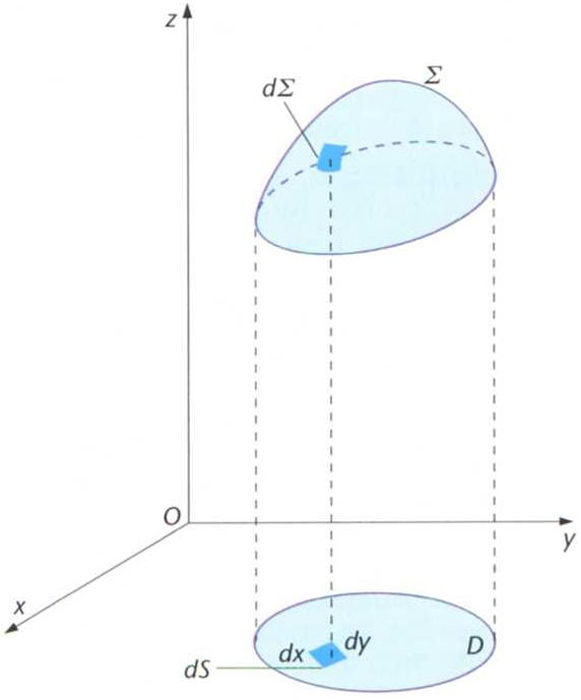
Element de superfície
© fototeca.cat
Matemàtiques
Cadascuna de les parts infinitesimals en què hom divideix una superfície a l’hora de calcular-ne l’àrea.
En coordenades cartesianes l’element de superfície dS val dS = dx dy , i en coordenades polars dS = ρ d ρ d θ L’àrea A d’una superfície regular z = f x,y que tingui com a projecció en el pla XOY un recinte S , és igual a la integral doble expressada per
mínim relatiu
Matemàtiques
Valor que pren una funció f(x) en un punt x=a quan aquest valor és menor que els valors de f(x) en els punts immediatament anteriors i posteriors al punt a.
És anomenat també mínim local , i en el cas particular que existeixen les derivades successives de f x es compleix que en el punt a la primera derivada f ' a és nulla i la segona, f ' a , normalment és positiva En el cas, però, que tant f ' a com f ' a siguin nulles, la condició que f x tingui un mínim en el punt a és que la primera derivada de f x no nulla en el dit punt sigui d’ordre parell i positiva Aquestes són les condicions que hom aplica per a trobar els mínims d’una funció
màxim relatiu
Matemàtiques
Valor que pren una funció f(x) en un punt x=a quan aquest valor és més gran que els valors de f(x) en els punts immediatament anteriors i posteriors al punt a.
És anomenat també màxim local, i, en el cas particular que existeixin les derivades successives de f x , es compleix que en el punt a la primera derivada f' a és nulla i la segona f' a normalment és negativa En el cas, però, que tant f' a com f' a siguin nulles, la condició que f x tingui un màxim en el punt a és que la primera derivada de f x no nulla en el dit punt sigui d’ordre parell i negativa Aquestes són les condicions que hom aplica per a trobar els màxims d’una funció
circumscriure
Matemàtiques
Traçar una figura que n’envolti una altra amb la qual tingui el major nombre de punts comuns possible.
Generalment hom circumscriu una corba superfície tancada a un polígon políedre que hi és contingut
sèrie de funcions
Matemàtiques
Successió de funcions {
F n
} amb
, on les
f i
són també funcions.
Hom la indica per Σ f n Si { F n } té per límit una funció f , hom diu que la sèrie Σ f n és convergent cap a la funció f i que f és la seva suma, dins el domini on això tingui sentit Si les f i són funcions potencials, f i x = a i x i , la sèrie Σ f n és anomenada sèrie de potències Si la variable x és complexa hom pot demostrar que hi ha un nombre positiu R tal que per a tot x tal que | x | < R la sèrie numèrica Σ a n x n és absolutament convergent, mentre que per a tot x tal que…
mètode de Montecarlo
Matemàtiques
Mètode estadístic pel qual, mitjançant un mostreig artificial (que en general utilitza successions de xifres aleatòries), hom arriba a estimar la probabilitat que un procés real tingui lloc.
L’ús d’un mostreig artificial o procés de simulació , que actualment és facilitat per la utilització d’ordinadors, evita el mètode analític de comptabilitzar totes les dades reals que concorren en el procés analitzat i que, a causa de llur quantia i aleatorietat, desborden les possibilitats de comptabilització El mètode de Montecarlo fou perfeccionat entre els anys 1950 i 1960, i té com a antecedent històric l’estimació feta per GBuffon, l’any 1773, de les xifres decimals del nombre pi π El mètode ha estat utilitzat amb èxit en física nuclear determinació de les dimensions crítiques d’un…
distribució
t
n
Matemàtiques
Siguin Y
i Z
variables aleatòries independents tals que Y
sigui N
(0,1) i Z
tingui una distribució x 2
amb n
graus de llibertat i hom consideri la variable aleatòria
Aquesta variable té la funció de distribució i densitat La funció de distribució S n x rep el nom de distribució t amb n graus de llibertat o de distribució Student amb n graus de llibertat en memòria de l’estadístic anglès WS Gosset, que escrigué amb el pseudònim de Student
subharmònic | subharmònica
Matemàtiques
Dit de qualsevol funció real de dues variables u(x,y) que tingui segones derivades parcials contínues en el seu domini de definició i que en cada punt d’aquest satisfaci l’equació: .