Resultats de la cerca
Es mostren 38 resultats
teorema de Rouché-Frobenius
Matemàtiques
Teorema que permet la classificació dels sistemes lineals d’equacions.
Donat un sistema no homogeni de m equacions lineals amb n incògnites, escrit en forma matricial A x = b , b ≠ 0 , on A és la matriu de coeficients del sistema, b la columna dels termes independents i x la columna de les incògnites, el sistema és compatible és a dir, que té solucions si el rang de A és igual al rang de la matriu ampliada A , b matriu Si aquest rang és igual al nombre d’incògnites, aleshores es tracta d’un sistema compatible determinat o sia, amb solució única, però si el rang és menor que el nombre d’incògnites, es tracta d’un sistema compatible indeterminat amb infinites…
allisatge
Matemàtiques
Conjunt de mètodes per al tractament de dades estadístiques de tipus cronològic o sèries temporals, que tenen per objecte fer previsions a curt termini basades en les dades anteriors.
Hom tracta de separar la fluctuació aleatòria de la llei subjacent del fenomen, allisant els valors històrics anteriors La més emprada és la tècnica anomenada de les mitjanes mòbils , que pren com a previsió la mitjana aritmètica de les N darreres dades Hom pot veure fàcilment que S t +1 = S t + X t — X t-N /N Si es tracta, p ex, de preveure les vendes d’un producte per al més següent t+ 1, hom pren la mitjana dels darrers dotze mesos, amb la qual cosa hom suposa que s’eliminaran les variacions aleatòries El mètode de l' allisatge exponencial representa una elaboració de l’anterior que…
cissoide de Diocles
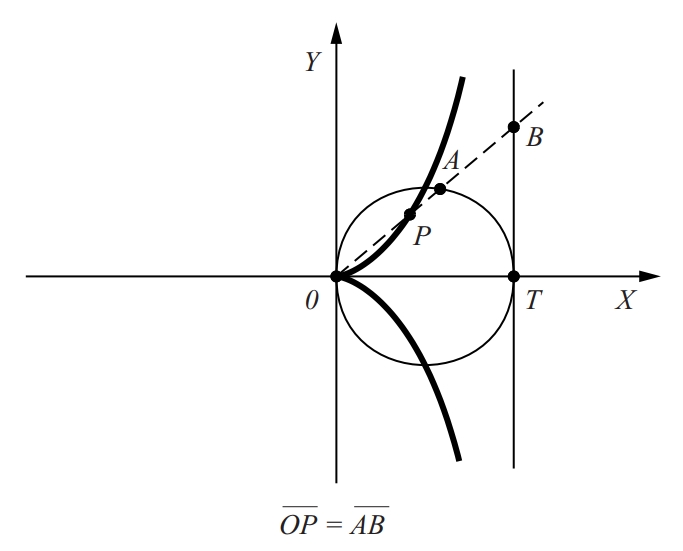
cissoide de Diocles
Matemàtiques
Cissoide associada amb una circumferència, a una recta tangent i a un punt fix O diametralment oposat al punt de tangència.
Fou construïda per Diocles per resoldre la duplicació del cub La seva equació cartesiana és y 2 2 k – x = x 3 Es tracta, doncs, d’una cúbica
representació
Matemàtiques
Donat un grup, grup (de permutacions, matrius o transformacions) que li és isomorf.
Quan hom tracta amb grups abstractes, sovint és interessant d’emprar una representació del grup , per tal d’operar millor amb ell Tot grup finit pot ésser representat per un grup de permutacions o de matrius
esfera
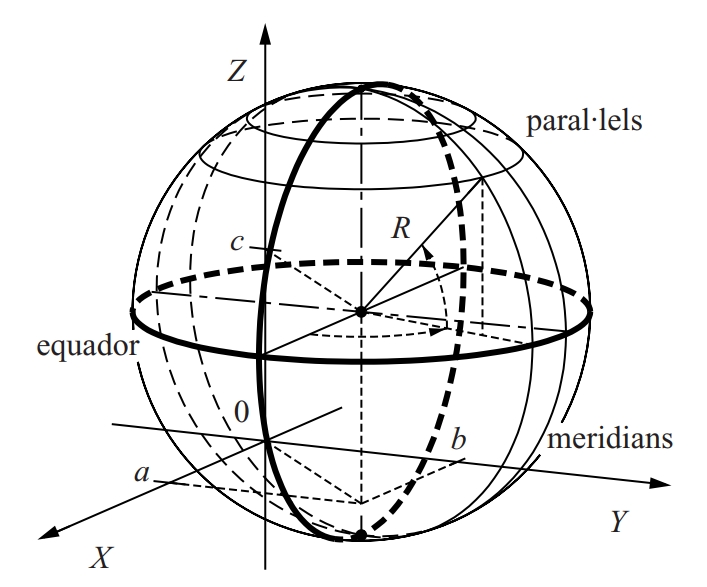
Esfera de centre (a, b, c) i radi R
Matemàtiques
Figura espacial generada per la rotació d’un cercle al voltant d’un dels seus diàmetres.
Es tracta d’una quàdrica amb equació cartesiana x – a 2 + y – b 2 + z – c 2 = R 2 si el centre és el punt a , b , c i el radi és R El seu volum val i la seva superfície S = 4 π R 2
lògica algèbrica
Matemàtiques
Estudi algèbric de la lògica com a llenguatge (metallenguatge).
La lògica algèbrica tracta, doncs, les estructures que presenten les diferents lògiques i d’aquesta manera arriba a trobar estructures algèbriques —poc usuals en l’àmbit de l’àlgebra clàssica— com són, entre d’altres, les àlgebres de Hilbert, de Heyting, d’Abbott, de Boole, de Wajsberg, monàdiques, poliàdiques i cilíndriques
gràfic | gràfica
Matemàtiques
Subconjunt del producte cartesià A × B de dos subconjunts; es tracta doncs, d’una colla de parelles d’elements (a, b), on a ∈A i b ∈B.
En el cas que A i B siguin, respectivament, el domini de definició i la imatge d’una funció, el gràfic corresponent és anomenat també gràfica funcional o corba associada a la funció
autòmat finit determinista
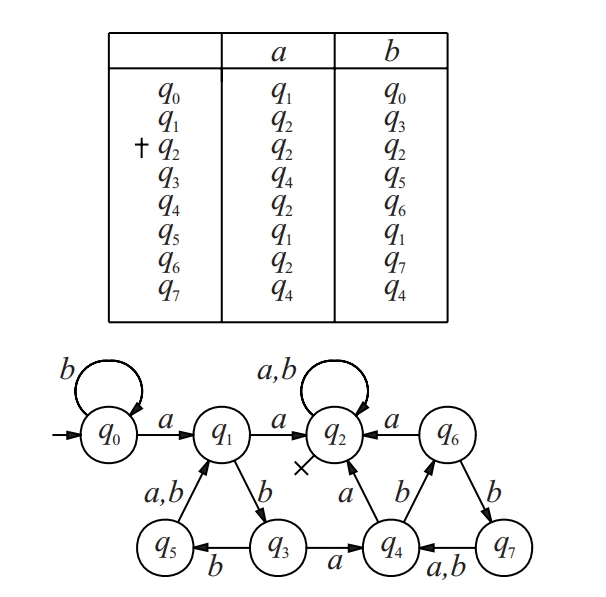
autòmat finit determinista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, q0, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet, anomenat d’entrada; δ : Q ⨉ ∑* → Q és la funció de transició que satisfà ∀q ∈ Q, ∀x,y ∈ ∑*:δ(q, λ) = q, δ(q, xy) = δ(δ(q, x), y) essent xy la concatenació de x i de y, i λ la paraula buida i ∑* el conjunt de paraules; q0 ∈Q s’anomena estat inicial; F ⊂ Q s’anomena conjunt d’estats finals o acceptadors.
Usualment un autòmat finit determinista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si δ q i , a = q j S’indica l’estat inicial amb una fletxa i els finals amb una creu
seminorma
Matemàtiques
Aplicació d’un espai vectorial E en el conjunt de nombres reals positius.
A tot vector x de E assigna un valor ∥ x ∥ de manera que ∥ a x ∥ = | a | ∥ x ∥, i que, per a tot x, y de E , ∥ x + y ∥ ≤∥ x ∥ + ∥ y ∥ Si una seminorma compleix, a més, que ∥ x ∥=0 implica x = 0, aleshores es tracta d’una norma En ℝ 2 el pla, ∥ x , y ∥ = | x + y | és una seminorma que no és norma Tota norma és seminorma, però no inversament
variable aleatòria
Matemàtiques
Aplicació mesurable d’un espai de probabilitat (Ω, A, P) en (ℝ, Bℝ), on ℝés el conjunt dels nombres reals i Bℝ la tribu de Borel corresponent.
Expressa el resultat d’un experiment aleatori En el cas que la funció prengui un nombre finit de valors en tot interval finit, hom diu que es tracta d’una variable aleatòria discreta en el cas contrari, la variable aleatòria és de tipus continu Si X és una variable aleatòria del tipus continu tal que la seva funció de distribució admet una densitat fx , hom té σ 2 X = ∫ ℝ x- E X 2 f x dx