Resultats de la cerca
Es mostren 12 resultats
equipol·lència
Matemàtiques
Relació d’equivalència entre vectors fixos de l’espai euclidià.
Dos vectors són equipollents si existeix una translació que transforma l’un en l’altre Les classes de vectors equipollents són anomenades vectors lliures vector
baró de Prony
Matemàtiques
Nom amb què és conegut Gaspard-Marie Riche, enginyer i matemàtic francès.
Transformà molts canals i ports i construí el port de la Concòrdia, de París És conegut sobretot pel fre dinamomètric que ideà, anomenat fre de Prony
modular
Matemàtiques
Dit del grup de transformacions del pla complex del tipus w = (az+b)/ (cz+d), essent a, b, c i d nombres enters que compleixen la condició ad-bc = +1.
Tota transformació d’aquest grup transforma el semiplà complex superior en ell mateix i deixa invariant l’eix real Aquest grup és utilitzat per a definir la funció modular J , que té un paper fonamental en l’estudi de les funcions ellíptiques
transposició
Matemàtiques
En una matriu, canvi de les files per les columnes.
Així, la matriu es transforma per transposició en El determinant d’una matriu quadrada és invariant per transposició Una matriu en què la inversa és igual a la transposada, és anomenada ortogonal aquestes matrius representen els moviments lineals que conserven distàncies, angles i productes escalars
semblança
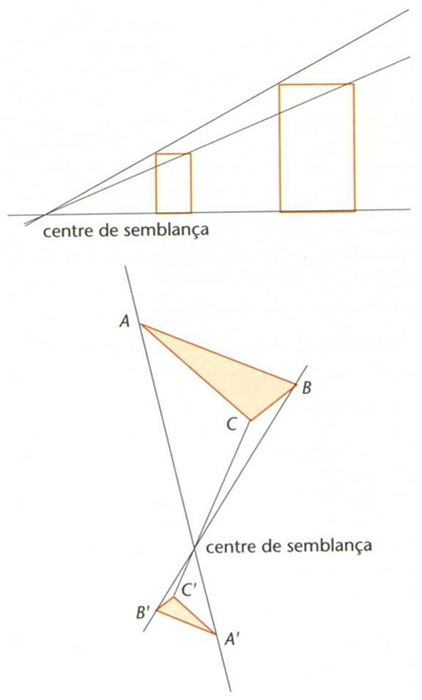
Dues semblances directes
© Fototeca.cat
Matemàtiques
Transformació geomètrica T de ℝn en ℝn tal que la distància entre les imatges de dos punts qualssevol és igual a la distància entre aquests dos punts multiplicada per una quantitat constant positiva dita raó de la semblança.
És a dir, d T x, T y = k, d x, y Dues figures són anomenades semblants si hi ha una semblança que transforma l’una en l’altra Les semblances conserven la forma de les figures però en canvien la grandària, eixamplant-la o reduint-la segons que la raó sigui respectivament major o menor que 1 Les semblances de raó 1 són dites isometries o moviments rígids , els quals són sempre el resultat de compondre una translació amb una transformació lineal ortogonal que conserva els angles Les homotècies són exemples típics de semblances Tota semblança és el resultat d’aplicar successivament una…
superposició
Matemàtiques
Principi geomètric segons el qual figures iguals admeten un moviment rígid o isometria que transforma l’una en l’altra.
Aquestes figures són dites superposables així, dos triangles de costats iguals ho són El principi de superposició permet de classificar les figures Aquest és l’objecte central de la geometria mètrica
forma
Matemàtiques
Aplicació f d’un espai vectorial E de n dimensions en el cos K d’escalars en el qual és definit i que generalment és el cos dels nombres reals o dels nombres complexos.
Segons quin sigui el valor de n i les propietats de f , hom distingeix diversos tipus de formes Hom diu que f és una forma lineal o funcional lineal si, per a x i y de E i λ de K, f satisfà f x+y = f x + f y i f λ x = λ f x El conjunt de formes lineals d’un espai vectorial E sobre el seu K , és E* , espai dual Si hom pot considerar E com a producte cartesià de n espais vectorials, una forma f transforma tot conjunt ordenat de n vectors en un escalar de K si aquesta f , en ésser restringida a un vector qualsevol, constitueix una forma lineal, f és anomenada forma multilineal Un cas…
projectivitat
Matemàtiques
Transformació projectiva, és a dir, aplicació injectiva entre dos plans projectius no necessàriament diferents (f: p* →p*’, que transforma conjunts de punts col·lineals en conjunts de punts col·lineals.
L’estudi de les propietats del pla projectiu invariants sota una projectivitat són l’objecte d’estudi de la geometria projectiva Si f és una projectivitat, es demostra que el transformat x' , y' d’un punt x , y es troba per les equacions i que tota transformació donada per les anteriors equacions és una projectivitat plana, és a dir, que els punts x, y tals que a 3 x + b 3 y + c 3 = 0 es transformen en els punts impropis del pla projectiu
subespai
Matemàtiques
Qualsevol subconjunt no buit F d’un espai vectorial E (sobre un cos K) tal, que és estable per a les dues lleis de E i que, proveït d’aquestes lleis induïdes, és també un espai vectorial (sobre K).
En l’espai vectorial de tres dimensions ℝ 3 els subespais són el mateix espai, l’origen de coordenades i totes les rectes i els plans que passen per l’origen F és un subespai de E si, donats qualssevol x , y de F i λ de K , aleshores la combinació lineal x ,-λ y pertany a F Tota família de vectors determina l’anomenada envolupant lineal , o mínim subespai, que els conté La intersecció M ∩ N de dos subespais M i N és un subespai, però la reunió M ∪ N no ho és en general La suma M + N definida per a tots els vectors que són suma d’un element de M i un de N és el mínim subespai que conté la…