Resultats de la cerca
Es mostren 12 resultats
angle entre varietats lineals
Matemàtiques
En el pla i l’espai, angle A(x̄,ȳ) entre dos vectors x̄,ȳ no nuls que es pot considerar com l’angle determinat per les semirectes generades pels vectors.
En termes del producte escalar s’obté x̄ ȳ = || x̄ || || ȳ || cos A x̄ , ȳ Per mitjà d’aquest concepte es pot precisar l’angle entre dues rectes, entre recta i pla, i entre dos plans
William Paul Thurston
Matemàtiques
Matemàtic nord-americà.
Féu estudis sobre la topologia i la geometria de varietats en tres dimensions, mitjançant deformacions dels seus grups d’isometria Medalla Fields 1983
Élie Cartan
Matemàtiques
Matemàtic francès.
Treballà en el camp de la teoria de grups Juntament amb HPoincaré, desenvolupà el càlcul de formes diferencials exteriors sobre varietats diferenciables, i avançà el concepte de fibrat
varietat lineal
Matemàtiques
Subconjunt F del conjunt de punts E d’un espai afí (E, V) tal, que per a tot punt X de F hom pot trobar un punt P de F i m vectors linealment independents v1, ..., vm , de manera que X = P + t1 v1 + ... + tm vm , on t1, ..., tm són nombres reals.
Els vectors v 1 , , v m formen un sistema de vectors directors de F , i el nombre m fixa la dimensió de la varietat Les varietats lineals de dimensió 1 són les rectes , i les de dimensió 2, els plans En general, en un espai afí de dimensió n , una varietat lineal de dimensió n -1 és anomenada hiperplà
Shigefumi Mori

Shigefumi Mori
© International Mathematical Union
Matemàtiques
Matemàtic japonès.
Graduat a la Universitat de Kyoto l’any 1975, es doctorà el 1978 amb una tesi sobre l’endomorfisme dels anells en variants abelianes Posteriorment fou professor assistent en aquesta universitat fins el 1980, que passà a la Universitat de Nagoya, on fou nomenat professor titular el 1988 L’any 1990 retornà a la Universitat de Kyoto, on ocupa una càtedra Des del 1977 ha estat professor visitant en diverses universitats dels EUA El seu interès se centra en la geometria algèbrica, i ha desenvolupat tècniques per tal de resoldre el problema de la classificació completa de les varietats…
reticle
Matemàtiques
Conjunt ordenat en el qual dos elements qualssevol tenen un suprem (la més petita de les fites superiors o elements majorants) i un ínfim (la més gran de les fites inferiors o elements minorants).
És anomenat també conjunt reticular Si C, ≤ és un “ordenat” que és reticle, donats a i b de C, existeix un element, anomenat suprem c = a ∪ b tal, que a ≤ c , b ≤ c , i si a < d i b < d és c < d i un element, dit ínfim , c = a ∩ b tal, que c < a, c < b i si d ≤a, d ≤ b , és d ≤ c El conjunt de parts d’un conjunt respecte a l’ordre definit per la inclusió és un reticle Exemple si A i B són dos conjunts qualssevol, el conjunt més petit que els conté és la seva reunió o suprem i el més gran contingut és la seva intersecció o ínfim La teoria de reticles nasqué amb l’estudi del…
Joan Girbau i Badó
Matemàtiques
Matemàtic.
Estudià ciències matemàtiques a la Universitat de Barcelona 1959-64 Després d’ocupar diverses places de professor en aquesta universitat, entre el 1970 i el 1972 es traslladà a París, on feu els primers treballs de recerca sota la direcció d’André Lichnerowicz Catedràtic de la Universitat Autònoma de Barcelona des del 1976, treballà en diverses recerques relacionades amb la geometria diferencial, especialment la cohomologia de les varietats complexes i la teoria de les foliacions holomorfes Del 1986 al 1990 presidí la Societat Catalana de Matemàtiques L’any 1990 fou elegit membre…
Heisuke Hironaka
Matemàtiques
Matemàtic japonès.
Estudià a la Universitat de Kyoto, on es graduà en ciències l’any 1954, i obtingué un màster l’any 1956 L’any 1957, a instàncies d' Oscar Zariski , anà a Harvard, on es doctorà el 1960 Posteriorment fou successivament professor a les universitats de Brandeis i Columbia fins el 1968, que es reincorporà a la Universitat de Harvard El 1975 retornà al Japó i fou nomenat professor a l’Institut per a la recerca matemàtica de la Universitat de Kyoto, que dirigí entre el 1983 i el 1985, i on es jubilà 1991 En el període 1996-2002 fou president de la Universitat de Yamaguchi, i posteriorment director…
angle
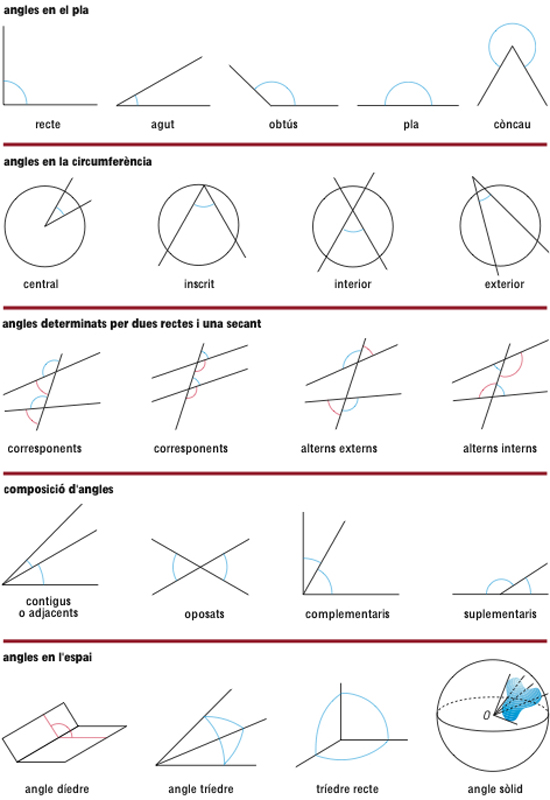
Diversos tipus d’angles
© Fototeca.cat
Matemàtiques
Regió del pla limitada per dues semirectes d’origen comú.
Per a mesurar angles hom utilitza diverses unitats l’angle recte, el grau sexagesimal, el grau centesimal i el radian El grau sexagesimal és obtingut dividint el cercle en 360 parts iguals El grau es divideix en 60 minuts i el minut en 60 segons Les abreviatures són ° grau, ′ minut, ″ segon Per exemple, 23° 27′ 35″ es llegeix 23 graus , 27 minuts i 35 segons El transportador d’angles permet fer mesures directes d’angles dibuixats en graus sexagesimals El grau centesimal és obtingut dividint l’angle recte en 100 parts iguals El grau es divideix en 100 minuts i el minut en 100 segons El símbol…
àlgebra de Lie
Matemàtiques
Estructura algebraica l’ús principal de la qual resideix en l’estudi d’objectes geomètrics com ara grups de Lie i varietats diferenciables.
Àlgebra E tal que la seva llei de composició x , y compleix les dues propietats següents per a tot x ∈ E , x , x = 0 i, per a cada terna x , y , z ∈ E , x , y , z + y , z , x + z , x , y = 0 Un exemple d’àlgebra de Lie el constitueix l’espai ℝ 3 dotat del producte vectorial L’estudi d’aquestes àlgebres és important per a l’estudi dels grups de Lie, ja que, a cada grup de Lie, se li pot associar una àlgebra de Lie