Resultats de la cerca
Es mostren 33 resultats
volum
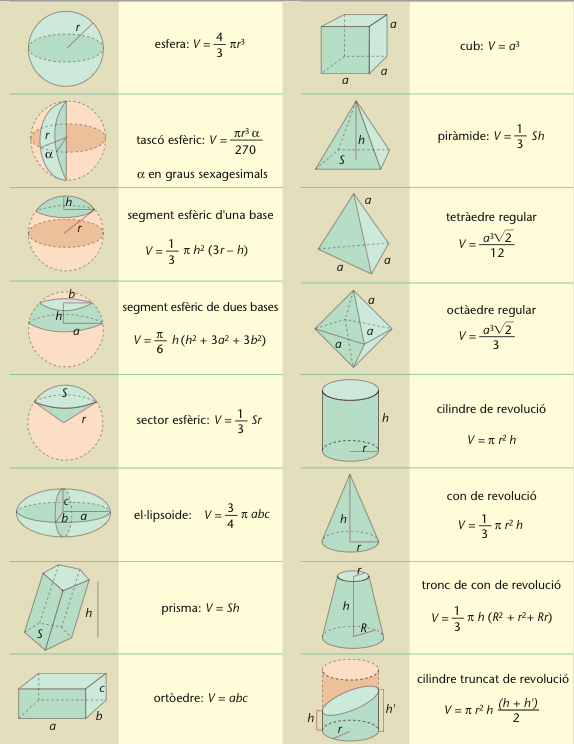
Fórmules per al càlcul de volums
© Fototeca.cat
Matemàtiques
Grandor o mesura de la porció de l’espai ocupada per un cos.
El volum és una mesura que a tota regió de l’espai de tres dimensions assigna un nombre real positiu, de manera que es compleix la propietat additiva, és a dir, que el volum d’un cos és igual a la suma dels volums de qualsevol partició que hom hagi fet en el cos divisió del cos en parts disjuntes Prenent com a base que el volum assignat a un cub de costat a és a 3 , el volum de qualsevol altre cos pot ésser calculat com l’ínfim de la suma dels volums dels cubs disjunts que plegats cobreixen el cos Així, el volum d’una figura…
teoremes de Guldin
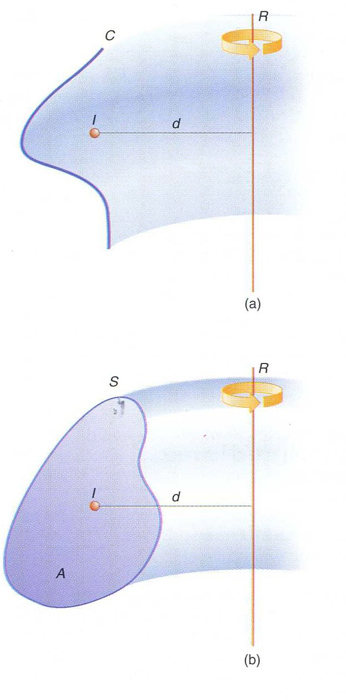
teoremes de Guldin: (a) primer teorema; (b) segon teorema
© fototeca.cat
Matemàtiques
Teoremes que relacionen el centre de massa d’una corba o d’una superfície amb l’àrea o el volum, respectivament, que generen en girar al voltant d’un eix.
Segons el primer teorema de Guldin , donada una corba plana C , de longitud l , que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2π dl , on d és la distància des del centre de massa I de la corba a la recta R en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material El segon teorema de Guldin afirma que, donada una superfície plana S , d’àrea A…
Teoría general de la urbanización
Matemàtiques
Obra teòrica i d’anàlisi estadística d’Ildefons Cerdà, publicada el 1867, per compte de l’Estat espanyol (reeditada en facsímil el 1968).
El primer volum inclou una història de la urbanització, un examen analític de l’estat contemporani de la urbanització, una anàlisi teoricohistòrica de les relacions entre sistemes de locomoció i formació de les urbs El segon volum correspon al títol secundari de l’obra Aplicación de sus principios y doctrinas a la reforma y ensanche de Barcelona Inclou un estudi del continent topografia, planta viària i interviària, alçat, organisme, del contingut població, del funcionament relacions continent/contingut i la científicament excellent Monografía estadística de la…
producte mixt
Matemàtiques
Donats tres vectors, a, b i c, nombre (a, b, c) donat per (a, b, c) = a·(b ∧c), on el signe ∧indica el producte vectorial.
Geomètricament representa el volum del parallelepípede determinat pels vectors a, b i c
ortòedre
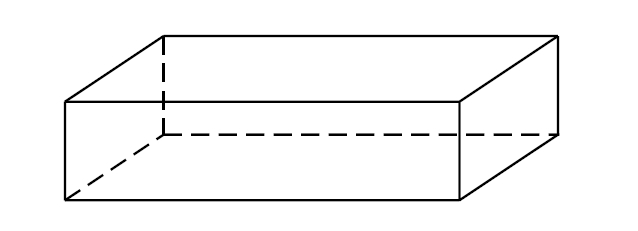
Ortòedre
Matemàtiques
Prisma de sis cares rectangulars que té tots els angles rectes.
Si les longituds de les arestes són a, b i c , la fórmula del volum de l’ortòedre és V=abc
sector esfèric
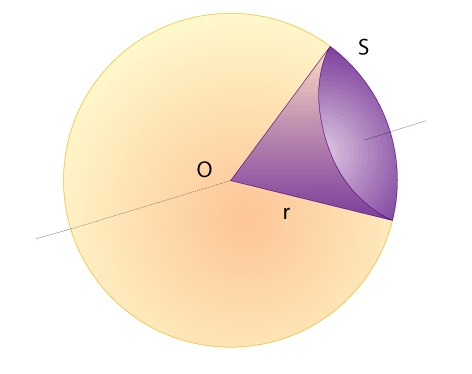
Sector esfèric
Matemàtiques
Part de l’espai limitada per una superfície cònica, que té el vèrtex en el centre d’una esfera, i la superfície de l’esfera.
Si S és la superfície de la part d’esfera que el limita i r n'és el radi, el volum del sector val V= 1/3 Sr
esfera
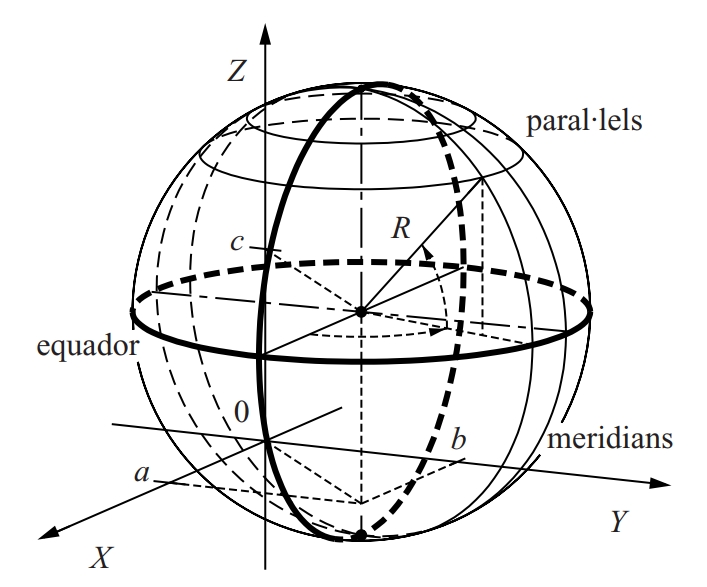
Esfera de centre (a, b, c) i radi R
Matemàtiques
Figura espacial generada per la rotació d’un cercle al voltant d’un dels seus diàmetres.
Es tracta d’una quàdrica amb equació cartesiana x – a 2 + y – b 2 + z – c 2 = R 2 si el centre és el punt a , b , c i el radi és R El seu volum val i la seva superfície S = 4 π R 2
tor
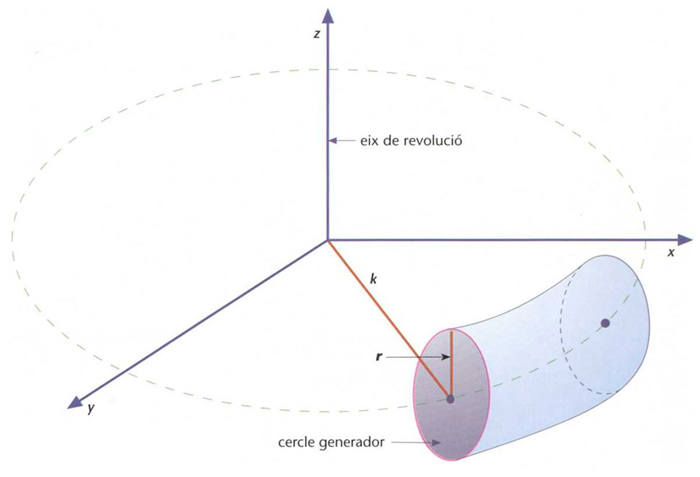
Generació d’un tor per un cercle
© Fototeca.cat
Matemàtiques
Superfície generada per la rotació, en l’espai, d’un cercle al voltant d’un eix del seu pla que no talla el cercle.
És la forma d’un anell de contorn circular i rodó Si r és el valor del radi del cercle generador, k la distància del centre a l’eix de revolució eix z , l’equació del tor és el seu volum val 2π kr, i l’àrea de la seva superfície, 4 π 2 kr