Resultats de la cerca
Es mostren 29 resultats
perspectiva

Caprici amb portalada a la vora del llac (segle XVIII-XIX), de Giacomo Guardi (Acadèmia Carrara, Bèrgam)
© Corel
Art
Disseny i arts gràfiques
Matemàtiques
Construcció geomètrica que permet de representar els objectes tridimensionals sobre una superfície bidimensional de forma que, quan és mirada amb un sol ull, immòbil i fixat a la distància justa, la imatge perspectiva coincideix amb la que en donaria la visió directa.
La perspectiva en l’art També hi són inclosos qualssevol mètodes o maneres de representar o suggerir la profunditat espacial sobre el pla pictòric Tot i que des del segle V aC els grecs ja degueren aconseguir algun sistema de formulació perspectiva més o menys plausible, i malgrat, encara, que des dels segles XIII i XIV circulaven, en la tradició dels tallers de pintors d’Itàlia i del nord d’Europa, esquemes geomètrics fragmentaris i fórmules empíriques de reducció perspectiva d’objectes aïllats o de plans parcials, només amb l’humanisme florentí s’obrí camí la perspectiva artificialis o la…
intuïcionisme
Matemàtiques
Corrent del pensament matemàtic, nascut a la segona meitat del s XIX.
Propugna que la matemàtica és l’estudi d’uns tipus de construccions mentals en les quals els objectes que hom maneja han d’ésser definits donant un criteri que en permeti la construcció i on el llenguatge emprat, sigui ordinari o simbòlic, només és un instrument auxiliar i no una part essencial de les construccions formalisme Hom accepta que la matemàtica intuïcionista és formada de tot allò que és conseqüència segons les normes de la lògica intuïcionista de la construcció de la successió dels nombres naturals ℕ, de la qual resulten evidents els axiomes de Peano base de la construcció formal…
Jeroni Cortès
Biologia
Matemàtiques
Matemàtic i naturalista.
Publicà, entre altres obres, Lunario y pronóstico perpetuo 1594, que fou reimprès moltes vegades fins a mitjan s XIX i esdevingué un dels llibres més populars impresos en llengua castellana, Libro de fisonomía natural 1598, també reimprès diverses vegades, resum dels coneixements de l’època en ciències naturals, que fou traduït al francès 1621 i al portuguès 1815, i Aritmética práctica 1604
Elements
Matemàtiques
Tractat de matemàtiques atribuït a Euclides i que ha estat, fins a mitjan segle XIX, l’autoritat màxima dins el camp de les matemàtiques generals.
Sintetitzà perfectament el treball dels antics matemàtics grecs i li donà una major coherència lògica amb les noves definicions de línia i de pla i, sobretot, amb la introducció del cinquè postulat millorà també l’ordenació i les demostracions de les proposicions Malgrat ésser un text de compilació, hom no pot posar en dubte que la planificació global de l’obra i el mètode expositiu, com també un bon nombre dels seus teoremes, són obra del mateix Euclides
postulat d’Euclides
Matemàtiques
Postulat cinquè del sistema de postulats d’Euclides, que, en llenguatge modern, diu que, donada una recta i un punt exterior, hom només pot traçar per aquest una recta paral·lela a la recta donada.
Aquesta proposició, enunciada per Euclides com a postulat, semblà als geòmetres posteriors que era demostrable a partir dels altres postulats del sistema, és a dir, que era un teorema Fins al s XIX se succeïren els intents de demostració sense resultat, fins que gairebé simultàniament Gauss, Bolyai i Lobačevskij tractaren de desenvolupar una teoria basada en els altres postulats d’Euclides i la negació del cinquè Si aquest hagués estat un teorema, la seva negació hauria conduït a una contradicció no tan sols no trobaren cap contradicció, sinó que obtingueren noves geometries, per…
Pablo Miquel Merino
Matemàtiques
Matemàtic.
Fill del català Pau Miquel i Costas, comerciant resident a l’Havana en el segle XIX A Cuba, estudià els primers estudis i el batxillerat, al Colegio de Belén Després d’aquesta etapa, passà tot seguit al País Basc, on estudià matemàtiques a la Universitat de Deusto Retornà a Cuba, on, el 1908, guanyà per oposició el càrrec d’ajudant facultatiu del gabinet d’astronomia Doctor en ciències fisicomatemàtiques, obtingué, el 1913, a la Universitat de l’Havana, la càtedra d’anàlisi matemàtica, on treballà durant més de 30 anys Entre la seva prolífica obra científica, cal destacar obres…
Augustus De Morgan
Lògica
Matemàtiques
Matemàtic i lògic anglès.
Fou professor de matemàtiques a l’University College de Londres 1828-66, excepte durant el període 1831-36, i el primer president de la London Mathematical Society, fundada l’any 1866 En un dels seus primers treballs, Elements of Arithmetic 1831, tractà, des del punt de vista filosòfic, dels conceptes de nombre i magnitud Les seves contribucions més importants són en el camp de la lògica simbòlica, i, juntament amb Boole, pot ésser considerat l’impulsor d’aquest nou corrent durant la primera meitat del s XIX En són remarcables, també, els treballs que fan referència a la…
Jean Gaston Darboux
Matemàtiques
Matemàtic francès.
La major part dels seus treballs es desenvoluparen en el camp de la geometria Publicà memòries sobre l’estudi de les superfícies ortogonals 1864-66, equacions diferencials de segon ordre en derivades parcials 1870 —per a les quals proposà un nou mètode d’integració—, aproximació de funcions, funcions discontínues, etc Una de les seves obres més importants, Leçon sur la théorie générale des surfaces et les applications géométriques du calcul infinitésimal 4 volums, 1887-96, constitueix una síntesi dels treballs duts a terme en els camps de la geometria i del càlcul durant el s XIX…
nombre complex
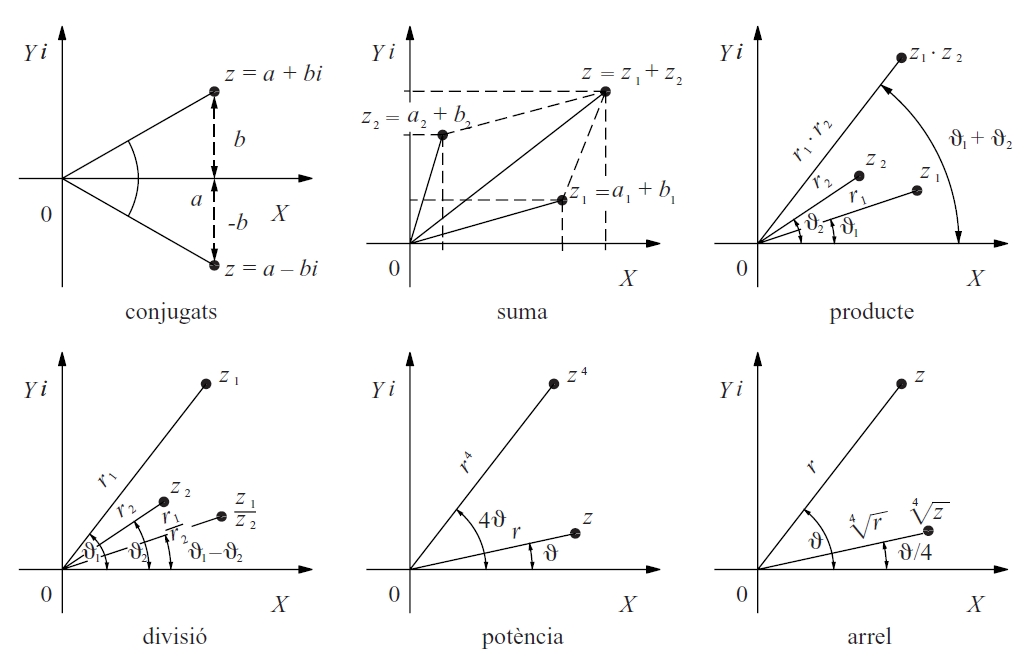
Nombres complexos
Matemàtiques
Nombre que pot ésser expressat com a suma d’un nombre real i d’un nombre imaginari.
Hom construeix el conjunt ℂ dels nombres complexos afegint al conjunt dels nombres reals un nombre nou, no real, que hom representa per una i , i que és definit formalment per la propietat que el seu quadrat és -1 Hom estén a aquest conjunt ℂ les operacions d’addició i de multiplicació amb totes les propietats que tenen entre nombres reals Cada nombre complex pot ésser escrit en forma de polinomi de primer grau en i , a + bi , i pot ésser representat geomètricament en el pla prenent a i b com a coordenades en un sistema cartesià ortogonal pla d'Argand-Gauss Aquesta correspondència entre els…
George Boole
Lògica
Matemàtiques
Matemàtic i lògic anglès.
Autodidacte, s’introduí en matemàtica mitjançant l’estudi de les obres de Lagrange i les de Laplace, i el 1849 obtingué una càtedra al Queen's College de Corcaigh Féu importants treballs en anàlisi matemàtica i contribuí a la fixació del llavors naixent concepte d’invariància Però la seva aportació més important fou l’inici de la lògica simbòlica És autor de The Mathematical Analysis of Logic 1847, The Calculus of Logic 1848 i de la seva obra mestra, An Investigation into the Laws of Thought, on which are Founded the Mathematical Theories of Logic and Probabilities 1854 El seu treball, que…