Resultats de la cerca
Es mostren 20 resultats
equació quadràtica
Matemàtiques
Equació de segon grau ax2 + bx + c = 0, o, en forma reduïda, x2 + px + q = 0.
Una equació quadràtica pura és la de la forma ax 2 + b = 0 En ax 2 + bx + c = 0, la fórmula de la solució és la quantitat b 2 - 4ac és anomenada discriminant
factor integrant
Matemàtiques
Funció M(x,y) que permet la integració d’una equació diferencial, per mitjà de la transformació d’aquesta en diferencial exacta.
Així, donada l’equació diferencial Ax,ydx + Bx,ydy = 0, multiplicant-la pel factor integrant Mx,y hom obté Mx,y Ax,y dx + Mx,y Bx,y dy = 0, que és diferencial exacta i, per tant, fàcilment integrable No sempre hi ha un factor integrant, i quan hi és, no és únic
mòdul
Matemàtiques
Estructura algèbrica constituïda per un conjunt M proveït d’una operació interna (+), respecte a la qual té estructura de grup commutatiu, i d’una operació externa (·) amb un anell unitari i commutatiu A
.
L’estructura satisfà, per a tot x , y ∈ M i a , b ∈ A , les següents propietats a bx = ab x a x + y = ax + ay a + b x = ax + bx 1 x = x La noció de mòdul és menys restrictiva que la d' espai vectorial la llei externa d’aquest requereix l’ús d’un cos en lloc d’un anell La noció de mòdul és menys restrictiva que la d' espai vectorial la llei externa d’aquest requeix l’ús d’un cos en lloc d’un anell Tot anell unitari és considerat un mòdul sobre ell mateix Si tot element del mòdul pot ésser expressat com a combinació lineal única d’una família de vectors del…
nombres conjugats
Matemàtiques
Dit de dos nombres algèbrics sobre un camp donat si són arrels de la mateixa equació irreductible amb coeficients en el camp.
Així, els nombres complexos a + bi, a-bi són conjugats sobre el camp real, puix que són arrels de l’equació X 2 - 2aX + a 2 + b 2 = 0
fórmula
Física
Matemàtiques
Expressió d’una relació entre diferents quantitats i magnituds mitjançant símbols.
Hom anomena especialment fórmula una relació, igualtat o desigualtat, remarcable Així, per exemple, la fórmula per a trobar les solucions de l’equació de segon grau ax 2 + bx + c = 0 és
discriminant
Matemàtiques
Invariant funcional que dóna una relació entre els coeficients d’un polinomi i que permet d’estudiar-ne les arrels i d’altres propietats.
En el cas d’un polinomi de grau n amb una sola variable, a 0 x n + a 1 x n - 1 + + a n , el discriminant és l’expressió En particular, el discriminant d’una equació quadràtica ax 2 + bx + c = 0 té com a expressió Δ = b 2 — 4 ac si Δ > 0, l’equació té dues arrels reals diferents, si Δ=0, té dues arrels reals iguals, i si Δ < 0, no té arrels reals sinó complexes
pla

Equació del pla
© fototeca.cat
Matemàtiques
Superfície tal que qualsevol recta que passi per dos dels seus punts es troba totalment continguda en la dita superfície.
Els plans, juntament amb els punts i les rectes, són els elements geomètrics primitius en l’axiomatització de Hilbert de la geometria D’altra banda, un pla és determinat per tres punts no alineats, o bé per dues rectes que es tallin o siguin paralleles, o bé per un punt i una recta que no contingui el punt A l’espai euclidià ℝ 3 un pla pot ésser representat per l’equació A x— x 1 + B y— y 1 + C z— z 1 = 0, en la qual x 1 , y 1 , z 1 són les tres coordenades d’un punt P 1 donat del pla, A, B, C són les tres components d’un vector N normal al pla, i x, y, z són les tres coordenades d’un…
paràbola
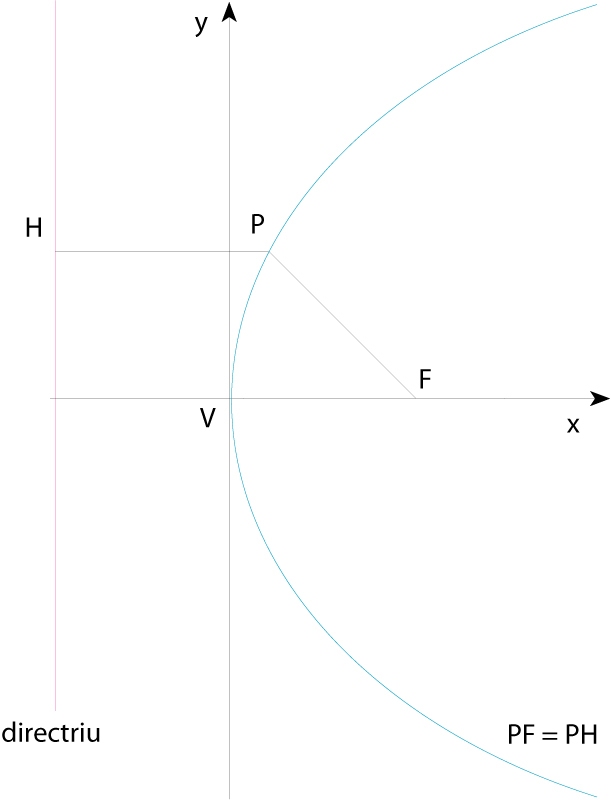
Paràbola (V vèrtex, F focus, P punt qualsevol de la paràbola)
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’una superfície cònica amb un pla paral·lel a una de les generatrius.
Constitueix el lloc geomètric dels punts del pla que equidisten d’un punt el focus de la paràbola i d’una recta que no conté el punt la directriu de la paràbola Té un eix de simetria que és la recta perpendicular que passa pel focus i que talla la paràbola en un punt anomenat vèrtex Referida a l’eix de simetria i a la seva perpendicular pel vèrtex, l’equació de la paràbola és y 2 =2 px , on p és la distància entre focus i directriu, anomenada paràmetre de la paràbola Hom pot demostrar que la gràfica de tota funció polinòmica de segon grau y= ax 2 + bx+ c és una paràbola de…
superfície
Matemàtiques
Conjunt de punts de l’espai que poden ésser determinats per dos paràmetres.
La manera més simple de determinar una superfície és donar una o més equacions del tipus z = f x,y Elegit un punt x,y en el domini de definició de la funció f , aquesta funció o aquestes funcions donen els valors de z , que, juntament amb x,y , són les coordenades cartesianes dels punts de la superfície Les funcions que donen la superfície esfèrica són , on el signe + correspon a l’hemisferi superior, i el signe - a l’hemisferi inferior L’equació z = ax + by + c correspon al pla o superfície plana Sovint és difícil, o impossible, d’expressar una superfície per mitjà de les…
regressió
Matemàtiques
Estudi de la millor aproximació d’una variable estadística y a partir d’una família donada de variables estadístiques x1..., xn, mitjançant combinacions lineals del tipus a1 x1..., an xn + b, i prenent com a criteri de “millor aproximació” el del mètode dels mínims quadrats.
Dit d’una altra manera, cal cercar els anomenats coeficients de regressió a 1 , a 2 , , a n , b , tals que facin mínima la distància al quadrat d 2 y, a 1 x 1 + + a n x n +b Si hom representa els valors de les variables estadístiques en l’espai ℝ n + 1 , aleshores l’hiperplà y = a 1 x 1 + + a n x n + b és dit de regressió per a n = 1, hom té la recta de regressió , i per a n = 2, el pla de regressió En el cas que n = 1, la recta de regressió y = ax + b té per coeficients on x i , y i són els valors de les variables, i x, y , les seves esperances o valors mitjans En el núvol de…