Resultats de la cerca
Es mostren 14 resultats
equació del transport
Física
Expressió matemàtica que fa el balanç dels guanys i pèrdues de partícules en un element de volum dV d’un medi en funció d’una direcció de desplaçament determinada r.
Té en compte les pèrdues clàssiques suma algèbrica de les entrades i les sortides que tenen lloc en la direcció r considerada, pèrdues degudes a les partícules que, per xoc dintre de l’element dV , han deixat de tenir la direcció r , pèrdues per absorció de partícules en el dV , guany de partícules en la direcció r per xoc en el dV i guany de partícules degut a l’existència eventual d’una font en el dV L’equació del transport, dita també de Boltzmann, és emprada en l’estudi de la difusió de partícules en un medi
volum
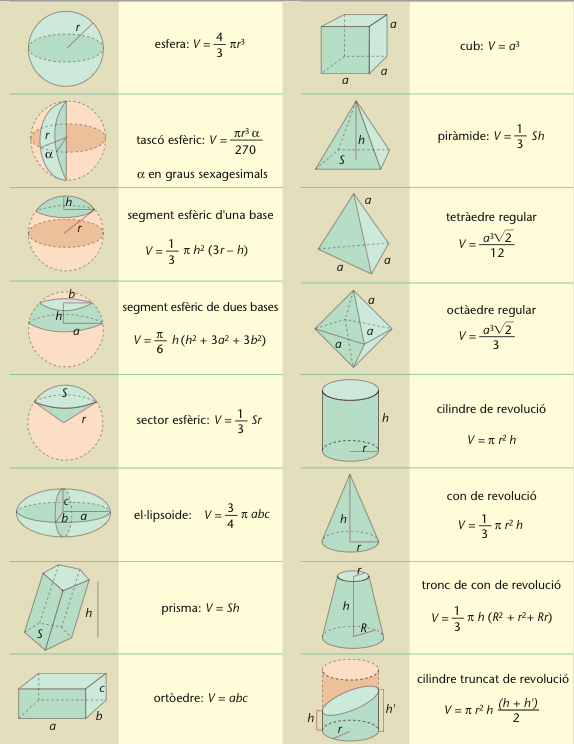
Fórmules per al càlcul de volums
© Fototeca.cat
Matemàtiques
Grandor o mesura de la porció de l’espai ocupada per un cos.
El volum és una mesura que a tota regió de l’espai de tres dimensions assigna un nombre real positiu, de manera que es compleix la propietat additiva, és a dir, que el volum d’un cos és igual a la suma dels volums de qualsevol partició que hom hagi fet en el cos divisió del cos en parts disjuntes Prenent com a base que el volum assignat a un cub de costat a és a 3 , el volum de qualsevol altre cos pot ésser calculat com l’ínfim de la suma dels volums dels cubs disjunts que plegats cobreixen el cos Així, el volum d’una figura plana és zero El volum dels cossos geomètrics simples…
densitat de càrrega elèctrica
Electrònica i informàtica
En un punt de l’espai en què hi ha una distribució de càrregues elèctriques, càrrega per unitat de superfície o volum.
En el primer cas, hom parla de densitat superficial de càrrega , σ= dQ/dS , i, en el segon, de densitat volúmica de càrrega , ρ= dQ/dV
nombre de Reynolds
Física
Coeficient sense dimensions, establert el 1883 per Osborne Reynolds, emprat en dinàmica de fluids, que caracteritza l’escolament d’aquests per una conducció i expressa la relació entre la força d’inèrcia i la de viscositat.
És donat per la relació Re = Dv ρ/μ, on D és el diàmetre interior de la conducció, v la velocitat d’escolament, ρ la densitat i μ la viscositat
filtració
Química
Operació de filtrar un fluid.
En la filtració, la fase líquida del sistema, per efecte d’un gradient de pressió, passa a través d’un suport permeable de paper, tèxtil, metàllic, etc, en el qual la fase sòlida és retinguda La substància sòlida acumulada en el suport forma una capa o pa que el cobreix i que actua de medi filtrant, en deixar passar el fluid pels nombrosos canalicles que el travessen En l’estudi de la filtració, per tal de poder construir els filtres adequats a cada necessitat, hom aplica la teoria de Buth o la de Carman, i cal la construcció de models experimentals i la posterior extrapolació dels resultats…
flux d’un camp vectorial a través d’una superfície
Matemàtiques
Donat un camp vectorial A i una superfície orientable S, integral de superfície de A sobre S
.
El flux elemental de A a través d’un element de superfície dS és el producte escalar d ϕ= A d S , on d S és el vector normal a dS i de mòdul dS El flux total de A a través de la superfície S és, doncs, Φ=∫∫ s A d S Si S és una superfície tancada que determina un volum V , la fórmula de Gauss o d’Ostrogadskij afirma que Φ = ∫∫ s A d S = ∫∫∫∂ x A x + ∂ y A y + ∂ z A z dV , on A x , A y i A z són les components del camp A
acceleració d’un punt
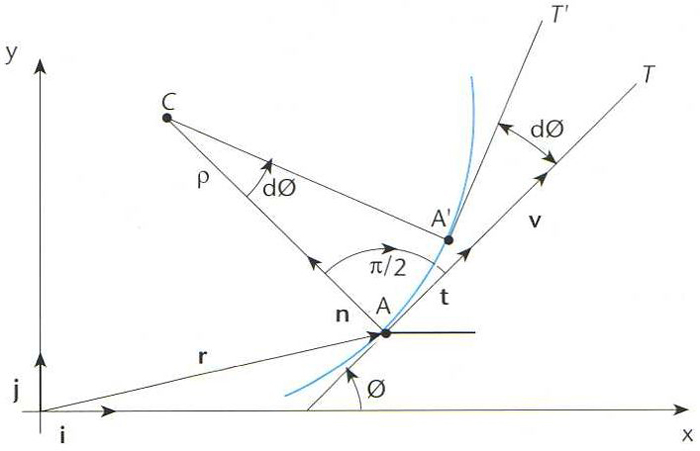
Acceleració d’un punt
© Fototeca.cat
Física
Variació de la velocitat del punt respecte al temps.
En el seu sentit més general és el vector a = < d v /dt , on v és el vector velocitat del punt del fet que v = d r /dt resulta que a = d 2 r /dt 2 , on r és el radi vector La unitat d’acceleració és el m/s 2 En termes dels vectors tangent t i normal n a la trajectòria, a pot escriure’s com a = dv/dt t + v 2 /ρ n , essent ρ el radi de curvatura La primera component és l’ acceleració tangencial és deguda al canvi de valor de la velocitat i la segona és l’ acceleració normal és deguda al canvi de la direcció de la velocitat En el cas d’un moviment rectilini, a = d 2 x/dt…
coet
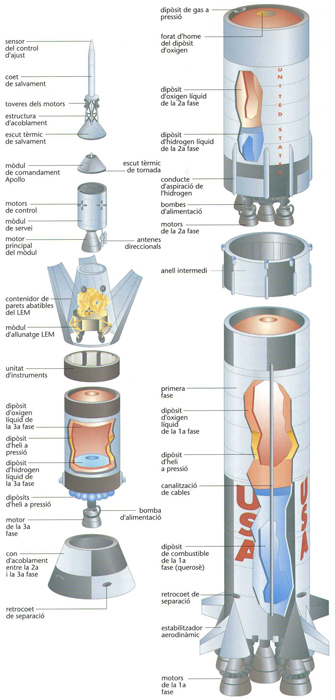
Saturn-V de tres fases amb mòdul d’allunatge (LEM)
© Fototeca.cat
Astronàutica
Grup autònom propulsat per l’ejecció de massa en una direcció determinada.
L’origen del coet és probablement oriental la primera notícia que hom té del seu ús és de l’any 1232, a la Xina Fou introduït a Europa pels àrabs Durant els segles XV i XVI fou emprat com a arma incendiària Posteriorment, amb l’extensió de l’artilleria, el coet bèllic desaparegué fins al segle XIX, que fou emprat de nou durant les guerres napoleòniques Els coets del coronel anglès William Congreve foren també usats a Espanya en el setge de Cadis 1810, en la primera guerra Carlina 1833-40 i durant la guerra del Marroc 1860 A la fi del segle XIX i el començament del segle XX, aparegueren els…
integració
Matemàtiques
Càlcul d’una integral.
Per a calcular integrals indefinides són útils, sovint, el mètode d’integració per substitució i el mètode d’integració per parts Segons el primer, hom fa x = φ t , i substitueix aquest valor a la integral ∫ f x dx = ∫fϕ t ϕ´ t dt , a fi de resoldre aquesta darrera més fàcilment El mètode d’integració per parts es basa en la relació → u dv = uv - que sigui de fàcil resolució Trobada la funció primitiva F x , la solució és ∫ f x dx = F x + C , on C és una constant La regla de Barrow proporciona un mètode general per a calcular integrals definides a partir de les…
coeficient de compressibilitat compressibilitar
Física
Quocient entre la disminució relativa del volum d’una substància i l’augment de pressió que l’ha produïda: k = —dV/VdP.
Es mesura en m 2 /N=Pa -1 Hom pot distingir el coeficient de compressibilitat isoterma , k T =—1/ V ∂ V /∂ P Ti el coeficient de compressibilitat adiabàtica , k S =—1/ V ∂ V /∂ P