Resultats de la cerca
Es mostren 27 resultats
subgrup engendrat per una part d’un grup
Matemàtiques
Si A és una part no buida d’un grup G, subgrup que resulta de la intersecció de la família de subgrups de G que contenen A.
Hom diu, aleshores, que aquest és el subgrup de G engendrat per A És, per tant, el menor subgrup de G que conté A
grup engendrat per una de les seves parts
Matemàtiques
Grup que coincideix amb el subgrup engendrat per una de les seves parts.
sòlid de revolució
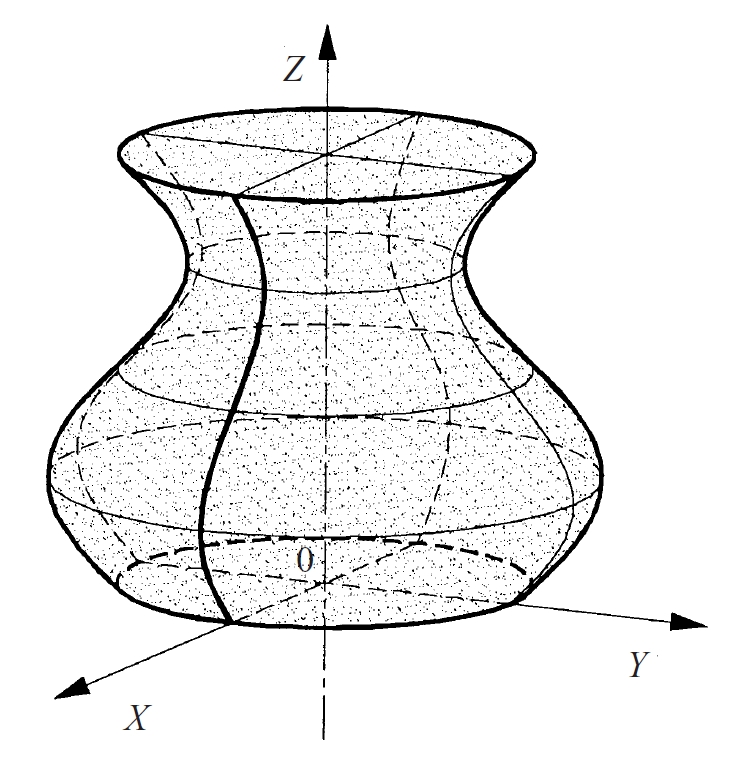
sòlid de revolució
Matemàtiques
Cos limitat per una superfície de revolució, que hom obté per la rotació d’una línia entorn d’un eix.
Així, l’esfera és el sòlid engendrat per un cercle que gira entorn d’un diàmetre el con de revolució és engendrat per una recta o un segment que talla l’eix al voltant del qual gira
procedir
Cristianisme
En teologia trinitària, provenir l’Esperit Sant del Pare (i del Fill, en la teologia llatina).
Genèricament es refereix també al Fill, per tal com és engendrat pel Pare
conjectures de Burnside
Matemàtiques
Conjunt de problemes algèbrics relatius als grups, plantejats per W.S.Burnside.
D’una banda, es preguntà si tot grup engendrat per un nombre finit d’elements i en el qual tot element és d’ordre finit és necessàriament finit aquesta conjectura fou resposta negativament per Novikov el 1959 D’altra banda, demostrà que si p i q són enters primers diferents, aleshores tot grup d’ordre p 2 q és grup resoluble
pare
El qui ha engendrat un o més infants.
terrigen | terrígena
cos complex
Matemàtiques
L’equació quadràtica x2 + 1 = 0 no té solució en el cos ℝ dels nombres reals.
Cal, doncs, construir un cos que contingui el cos ℝ com a subcòs i alhora un element i que compleixi i 2 + 1 = 0 Per fer-ho és possible procedir de dues formes D’una banda, és possible de considerar el pla complex D’una altra, és possible de considerar l’anell quocient ℂ = ℝ X / x 2 + 1, on ℝ X és l’anell dels polinomis en la variable X amb coeficients reals i X 2 + 1 és l’ideal engendrat pel polinomi, irreductible a ℝ, X 2 + 1 Hom disposa aleshores de l’aplicació canònica π ℝ X → ℂ i la imatge d’ X és anomenada i És a dir, i = π X Aquest cos té una propietat molt important…