Resultats de la cerca
Es mostren 29 resultats
teorema de Fermat
Matemàtiques
Teorema segons el qual si p és un nombre primer i a un nombre primer amb p, aleshores es satisfà que ap-1—1 és divisible per p, o sigui, ap-1≡(mod p).
La primera demostració d’aquest teorema fou feta per Euler el 1736
gran teorema de Fermat
Matemàtiques
Teorema segons el qual l’equació xn + yn = zn (n essent un nombre enter major de 2) no té solució entera distinta de la x = y = z = 0.
Fermat afirmà que havia trobat una demostració tot llegint un llibre de Diofant El 1983, l’anomenada conjectura de Fermat fou provada per a n≤ 125 000, i el 1995 el teorema fou resolt pel matemàtic anglès, resident als EUA, Andrew John Wiles
problema de Fermat
Problema de Fermat
© fototeca.cat
Matemàtiques
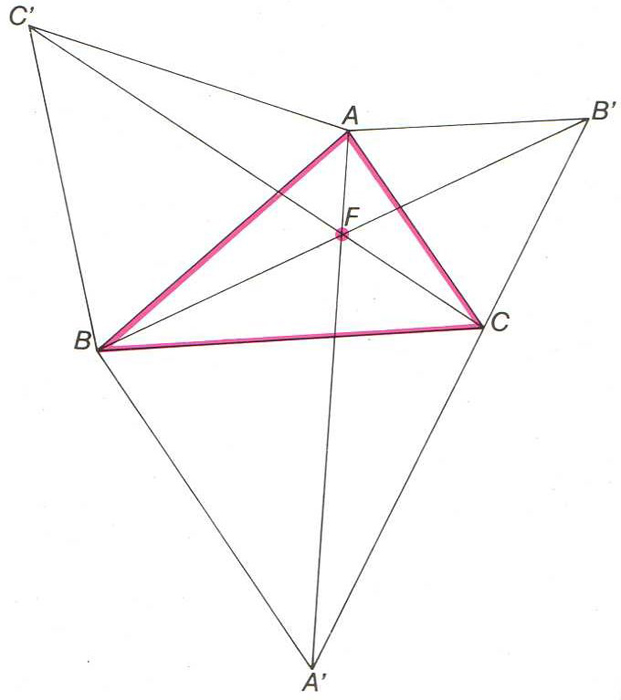
Donat un triangle ABC, problema que consisteix a trobar un punt M del pla per al qual la suma MA + MB + MC, és mínima.
El problema admet com a solució el punt de Fermat , si els tres angles del triangle són menors que 120°
nombres de Fermat
Matemàtiques
Nombres, Fn, definits per l’expressió (per a n = 1,2,3,...).
El 1640 Fermat cregué que aquests nombres eren primers, però l’any 1740 Euler donà una descomposició per a F 5 = 4 294 967 297, com a producte de 641 per 6 700 417, i posteriorment hom ha demostrat que per a n tal que 5 ≤n≤17 , F n no és primer, i que d’altres nombres de Fermat, com F 1 9 4 5 , F 3 3 1 0 i F 6 5 3 7 són descomponibles El 1796 Gauss demostrà que els únics polígons regulars que hom pot construir amb regle i compàs són els que tenen un nombre de Fermat de costats
punt de Fermat
Matemàtiques
Donat un triangle ABC, punt de concurrència F de les rectes AA’, BB’ i CC’ determinades gràcies als triangles equilàters exteriors ABC’, ACB’ i BCA’.
principi de Fermat
Física
Principi de l’òptica geomètrica segons el qual el camí òptic recorregut per un raig lluminós entre dos punts té un valor extrem, màxim o mínim, respecte a qualsevol altre camí òptic que hom pugui considerar entre aquests dos punts.
Com a conseqüència, el temps que el raig lluminós inverteix a anar d’un punt a un altre és mínim
espiral d’Arquimedes
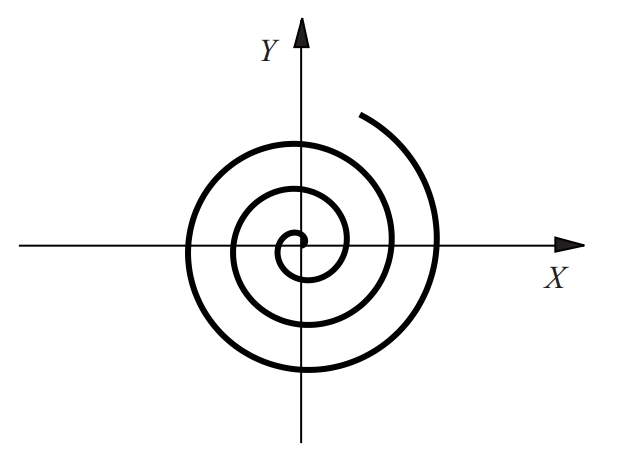
espiral d’Arquimedes (m = 1)
© fototeca.cat
Matemàtiques
Corba plana transcendent d’equació polar rm = kmθ.
En el cas de l’espiral clàssica d’Arquimedes, m = 1, però també són espirals d’Arquimedes l’espiral de Fermat, on m = 2, i l’espiral hiperbòlica o recíproca, on m = -1
espiral
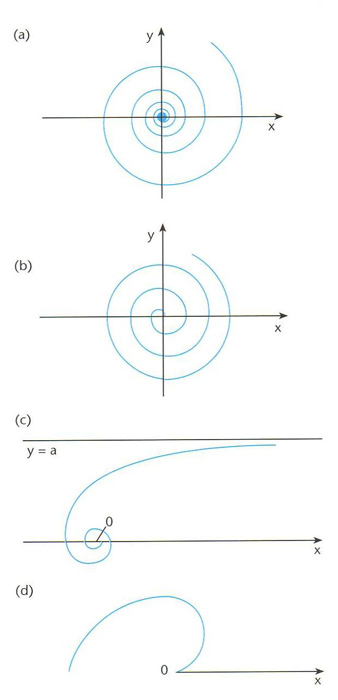
espiral: (a) logarítmica; (b) d’Arquímedes; (c) hiperbòlica; (d) parabòlica
© fototeca.cat
Matemàtiques
Corba plana descrita per un punt que gira al voltant d’un punt fix allunyant-se contínuament segons una llei determinada, característica per a cada tipus d’espiral.
Analíticament són representades gairebé sempre en coordenades polars Les equacions de les espirals més importants són espiral logarítmica o equiangular, r = e aθ espiral d’Arquimedes , r = r o /2πθ espiral hiperbòlica, r θ = a /θ espiral parabòlica o de Fermat, r 2 = a θ, i espiral sinusoidal, r n = a n sin n θ
sínia

sínia , al Baix Ebre
© Fototeca.cat
Física
Màquina d’elevar aigua, especialment emprada per a treure l’aigua de pous poc profunds.
Consisteix en una roda horitzontal, accionada per un animal que dóna voltes fermat a l’extrem d’un pal horitzontal solidari amb el seu eix, que engrana amb una altra roda vertical que mou una cadena sense fi, proveïda de catúfols en tota la seva llargada, l’extrem inferior de la qual és submergida a l’aigua del pou
principi variacional
Física
Proposició segons la qual un sistema físic macroscòpic aïllat de l’exterior evoluciona de manera que fa extremal la integral de la funció que el representa dinàmicament, calculada entre l’estat inicial i el final.
Quan el principi variacional és aplicat a la funció de Lagrange de la mecànica hom l’anomena principi de la mínima acció, o de Hamilton , i si és aplicat a la trajectòria d’una ona electromagnètica en resulta el principi de Fermat , mentre que si ho és a un procés de reacció exotèrmic és anomenat principi de Thomsen-Berthelot