Resultats de la cerca
Es mostren 39 resultats
longitud de difusió
Física
En la teoria dels reactors nuclears, magnitud proporcional al trajecte quadràtic mitjà recorregut per un neutró a l’estat tèrmic.
O, matemàticament parlant, distància a la qual el flux inicial de les partícules que es difonen resta dividit per e , en el cas de plantejar el problema amb una sola dimensió
curvatura de l’espai
Astronomia
Física
En el marc de la relativitat general, propietat geomètrica de l’espaitemps per la qual aquest es corba a causa de la presència de matèria.
El moviment de les masses és entès com un moviment lliure al llarg de les geodèsiques de l’espaitemps, en lloc d’ésser-ho en termes de la interacció gravitacional El tensor de curvatura explicita matemàticament aquesta propietat
coeficient de sensibilitat
Tecnologia
Capacitat d’un dispositiu per respondre a una excitació.
És mesurada matemàticament entre dos canvis absoluts, és a dir, pel quocient entre la magnitud de la resposta de l’instrument i la magnitud del senyal que cal mesurar, i és expressada normalment en divisions/volt o mm/A
mapamundi
Mapamundi, 2008
© Fototeca.cat
Cartografia
Mapa que representa la superfície de la Terra dividida en dos hemisferis.
A l’antiguitat hom ja en construí, bé que només se’n conserven a partir de l’edat mitjana, entre els quals té un gran interès l’Atles català Des del segle XVI els mapamundis són establerts matemàticament projecció de Mercator Actualment, hom utilitza les projeccions de Mercator, l’ortogràfica, l’estereogràfica, etc projecció
fenètica
Biologia
Tècnica de taxonomia numèrica que compara grups d’organismes a partir de la descripció de tantes característiques com siguin possibles per establir el grau de similitud entre aquests grups.
Preferiblement es descriuen més d’un centenar de característiques a les quals s’assignen valors numèrics que es tracten matemàticament per obtenir el grau de similitud entre taxons S’utilitza sovint per a classificar microorganismes, en els quals no es reconeixen gaires caràcters morfològics distintius, però sí fisiològics, que són quantificats d’aquesta manera
vibració
Física
En un sistema físic, moviment periòdic dels punts materials que el componen, originat per una font d’energia mecànica que provoca deformacions elàstiques i l’aparició de forces externes o internes que mantenen el moviment o el frenen.
L’estudi dels fenòmens vibratoris consisteix en l’anàlisi del comportament elàstic dels cossos sotmesos a moviments ondulatoris per això, la forma general d’expressar matemàticament una vibració és la combinació lineal de funcions sinusoidals La vibració d’un cos edificis, màquina, etc pot ésser l’origen de danys irreversibles en la seva constitució i el seu comportament, que són funció de l’amplitud, la velocitat, l’acceleració i la freqüència de la vibració, i a la vegada pot produir malestar o lesions físiques o psíquiques en l’home que hi resta sotmès
mètode dels elements finits
Matemàtiques
Mètode numèric per a resoldre problemes d’equacions diferencials en derivades parcials.
Matemàticament és una extensió de la tècnica de Rayleigh-Ritz-Galerkin el problema es planteja en forma variacional i hom aproxima la solució mitjançant una combinació lineal de funcions senzilles, en aquest cas funcions polinòmiques a trossos, nulles excepte en un petit domini dintre del qual són polinomis de grau baix El mètode aparegué els anys seixanta entorn de l’aplicació dels ordinadors als càlculs elàstics d’estructures, superà molt de pressa els mètodes de diferències finites i amplià ràpidament el seu camp d’aplicacions i es mostrà molt potent especialment quan la geometria del…
població estable
Sociologia
Model teòric de població tancada (sense entrades ni sortides migratòries) amb una estructura per edats i sexe fixa en el temps i amb un ritme de creixement (positiu o negatiu) constant.
Aquest model és el resultat de simular matemàticament el manteniment de taxes de mortalitat i de fecunditats inalterades durant moltes dècades, fins que l’única característica que varia és la grandària de la població Els fonaments teòrics d’aquest model ja els posà el matemàtic Leonhard Euler el 1760, però el seu desenvolupament definitiu arribà al s XX amb els treballs d’Alfred JLotka, aplicats extensament durant la segona meitat de segle en l’estudi de poblacions que no disposen de fonts estadístiques completes sobre la seva població Un cas particular de població estable és la…
osculador | osculadora
Matemàtiques
Dit de la corba o la superfície que, en un punt determinat, té el major contacte possible amb una altra corba o superfície.
Matemàticament, el pla osculador d’una corba guerxa és definit com el pla que adopta la posició límit dels plans determinats per tres punts veïns de la corba quan dos d’ells tendeixen a l’altre Si r = r t és l’equació paramètrica de la corba, l’equació del pla osculador en el punt r - r t 0 × r ´ t 0 r ´´ t 0 = 0, on les primes indiquen derivades temporals En les corbes planes, el pla osculador es redueix al pla de la corba L' esfera osculadora d’una corba guerxa és definida com l’esfera que adopta la posició límit de les esferes determinades per quatre punts de la corba…
mètode dels mínims quadrats
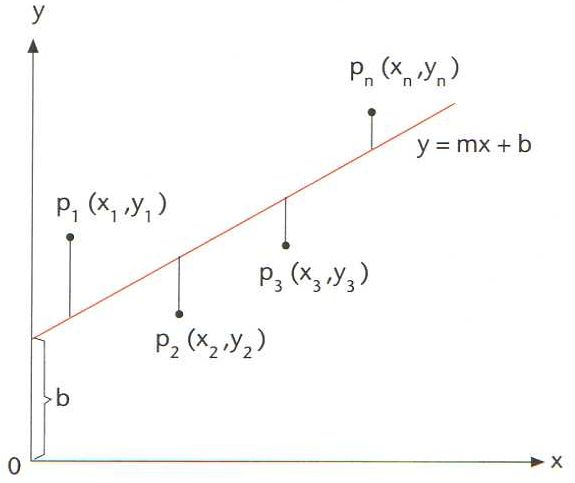
Representació de la recta y=mx + b obtinguda pel mètode dels mínims quadrats
© Fototeca.cat
Matemàtiques
Donat un conjunt de n punts del pla (x1, y1), (x2, y2), ... (xn, yn), mètode que permet de trobar l’equació y = mx + b de la recta que compleix la condició d’ésser la que més s’apropa als punts donats.
Hom defineix matemàticament la dita condició exigint que la suma dels quadrats de les desviacions, ha d’ésser mínima, entenent per desviació en un punt x i , y i la diferència d i = y i - mx i + b Hom pot demostrar que aquella condició condueix a les dues equacions a partir de les quals hom pot calcular els coeficients m i b de la recta, la qual és anomenada també recta de regressió D’altra banda, el mètode dels mínims quadrats serveix també per a ajustar funcions més complexes que la d’una recta, tals com funcions polinòmiques, exponencials, etc, i és utilitzat en l’estudi…