Resultats de la cerca
Es mostren 5896 resultats
funció conjugada d’una funció
Matemàtiques
Donada una funció f: D→ℂ, on D⊂ℝo D⊂ℂ, funció fD→ℂ definida per f( x)=f(x).
Òbviament, f és la funció conjugada de ff i f són mútuament conjugades
funció d’avaluació
Matemàtiques
Donats dos conjunts A, B i un conjunt F de funcions de A en B, funció αF , A: F×A→B definida per (f,a)→f(a) on f∈F i a∈A
.
Hom diu que α F , A és la funció d’avaluació de F respecte a A
integral indefinida
Integrals indefinides de les funcions usuals
©
Matemàtiques
Donada una funció f:(a,b] ⊂ℝ→ℝ, funció F definida en [a,b] per la integral (definida) F(x)= ∫fxsup;a&(t)dt.
Aquesta funció és una funció primitiva de la funció f , per tal com la seva derivada és igual a f , F' x = f x , i, de fet, genera la resta de funcions primitives de f , G x = F x + C , essent C una constant
funció inversa d’una funció
Matemàtiques
Donada una funció f(x), funció g(x) que satisfà (f₀g) (x)=(g₀f) (x)=x, on ₀és la composició de funcions: (f₀g)(x)=f[g(x)).
La funció inversa de f és representada, generalment, per f - 1 , i hom diu que composta amb f dóna la identitat En són exemples, la funció logarítmica, que és la inversa de la funció exponencial, o la funció arcsinus que és la inversa de la funció sinus
sèrie de funcions
Matemàtiques
Successió de funcions {
F n
} amb
, on les
f i
són també funcions.
Hom la indica per Σ f n Si { F n } té per límit una funció f , hom diu que la sèrie Σ f n és convergent cap a la funció f i que f és la seva suma, dins el domini on això tingui sentit Si les f i són funcions potencials, f i x = a i x i , la sèrie Σ f n és anomenada sèrie de potències Si la variable x és complexa hom pot demostrar que hi ha un nombre positiu R tal que per a tot x tal que | x | < R la sèrie numèrica Σ a n x n és absolutament convergent, mentre que per a…
caça bombarder
Caça bombarder F-18 de la Northrop-McDonnell Douglas (EUA)
© Fototeca.cat
Militar
Avió especialitzat a realitzar atacs contra objectius terrestres; també rep el nom de bombarder tàctic, avió d’atac ràpid o de suport reduït.
En anglès hom els designa amb les sigles FGA fighter, ground attack , que pressuposen la missió de caça, capacitat que tenen la majoria d’avions moderns d’aquest tipus per raó de la polivalència que cada cop més s’exigeix als costosíssims aparells actuals i així, els models nord-americans F-4, F-15 i F-18 , els soviètics SU-17 i MIG-25 , i els europeus Jaguar i Tornado són avions preparats per al combat aeri Dels concebuts exclusivament per atacar objectius terrestres cal esmentar l’ A-10A ‘Thunderbolt’ EUA, bireactor armat amb un canó automàtic de 6…
equació de Riccati
Matemàtiques
Equació diferencial de la forma y´ = dy/dx = f1(x) + y f2(x) + y2 f3(x).
No té una solució general calculable per quadratures, però si hom en coneix una solució particular y 0 , aleshores és fàcil de trobar-ne la solució general Fent el canvi y = y 0 + z , resulta l' equació de Bernoulli z´ = z f 2 x + 2 f 3 x y 0 + z 2 f 3 x , i fent el nou canvi u = 1/ z , hom n'obté una equació diferencial lineal d’integració immediata
funció còncava
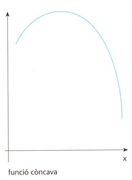
Funció concàva
© Fototeca.cat
Matemàtiques
Funció f:(a,b)⊂ℝ→ℝtal que per a tot α∈(0,1) se satisfà f(αx+(1—α)y)≥αf(x)+(1—α)f(y), on a<x<b i a<y<b.
El significat geomètric és que per a tot interval x,y ⊂ a,b la corda que uneix f x amb f y és situada per sota de l’arc que uneix f x amb f y
teorema de Schwarz
Matemàtiques
Teorema referit a una funció real f de dues variables reals, f: ℝ2 → ℝ.
Afirma que si existeixen les derivades primeres ∂ f /∂ x i ∂ f /∂ y en un entorn U d’un punt x 0 , y 0 , i existeix la derivada segona ∂ 2 f /∂i> x∂ y i és contínua en el punt x 0 , y 0 , aleshores existeix la derivada segona ∂ 2 f /∂ y ∂ x al punt x 0 , y 0 i se satisfà que ∂ 2 f /∂ x ∂ y x 0 y 0 = ∂ 2 f / ∂ y ∂ x x 0 , y 0 El teorema de Schwarz és una simplificació del teorema de Bonnet
jacobiana (d’una funció)
Matemàtiques
Donada una funció vectorial de diverses variables reals, f
: U
⊂ℝ m
→ℝ n
, que fa l’assignació f
: x
= (
x 1
,...,x m
) →f( x
) = (
f 1
( x
),...
f n x , matriu formada per les derivades parcials de la funció, és a dir, matriu els elements de la qual són J i j = ∂ f i /∂ x j Rep el seu nom del matemàtic Karl Jacobi