Resultats de la cerca
Es mostren 243 resultats
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar A partir de…
entrellaçament quàntic
Física
Propietat d’alguns estats quàntics de sistemes amb més d’una partícula, segons la qual l’estat del sistema complet no es pot representar com el producte directe d’estats separats per a les diverses partícules constituents.
D’acord amb el teorema de Bell, els estats entrellaçats poden presentar correlacions més fortes que no els estats clàssics per això se'ls considera ingredients ideals per a la computació quàntica L’existència d’aquests estats entrellaçats és fruit del principi de superposició de la mecànica quàntica i, d’acord amb l’argument d’Einstein-Podolskij-Rosen, implicaria que aquesta és incompatible amb una representació de la realitat basada en el principi d’acció local Les mesures experimentals relatives a les desigualtats de Bell donen suport a la mecànica quàntica El 1997 s’aconseguí…
Javier Muguerza Carpintier
Filosofia
Filòsof andalús.
Es llicencià en filosofia 1963 a la Universitat de Madrid, on es doctorà 1965 amb la tesi La filosofía de Frege y el pensamiento contemporáneo Professor a les universitats de Madrid 1963-65, Autònoma de Madrid 1965-72 i de La Laguna 1972-77, fou catedràtic de la Universitat de Barcelona 1977-79 i d’ètica de la Universidad Nacional de Educación a Distancia UNED 1979-2006 Fou director de l’Institut de Filosofia del Consell Superior d’Investigacions Científiques CSIC 1986-90 És considerat el principal introductor i propagador de la filosofia analítica a l’…
Terence Tao
Matemàtiques
Matemàtic australià.
Fill d’emigrants de Hong Kong Graduat 1991 i màster 1992 per la Universitat de Flinders, el 1996 es doctorà per la Universitat de Princeton Professor de la Universitat de Califòrnia Los Angeles UCLA des del 1996, els seus camps de recerca inclouen, entre d’altres, l’anàlisi harmònica, les equacions diferencials parcials, la combinatòria algèbrica, la combinatòria aritmètica, la combinatòria geomètrica, la teoria de probabilitats, la compressió de dades i la teoria dels nombres En aquest camp, el 2004 enuncià, conjuntament amb el matemàtic britànic Ben J Green, el teorema de…
càlcul de diferències
Matemàtiques
Estudi de les propietats d’una funció de la qual hom només coneix un conjunt finit de valors f(x0), f(x1), ..., f(xn), que corresponen als arguments x0, x1, ..., xn, els quals, habitualment, són presos en progressió aritmètica xr=x0+rϖ.
Hom defineix l’ operador diferència Δ, mitjançant l’expressió Δf x = f x + ϖ - f x , i l’ operador incremental E , definit per E ϖ f x = f x + ϖ = f x + Δ f x , de manera que E = 1+Δ Les propietats d’aquests permeten d’assolir el resultat següent, dit teorema de Gregory f x + nϖ = E nϖ f x = 1+Δ n f x , on, en l’última expressió, hom pot emprar la fórmula del binomi de Newton Aquests operadors poden expressar les diferències dividides Hom pot obtenir una aproximació polinòmica a la funció f x amb la fórmula d’interpolació de Newton en la qual, si f x és n…
Carl Friedrich Gauss
Carl Friedrich Gauss
Matemàtiques
Matemàtic alemany.
De família humil, extraordinàriament dotat per a les matemàtiques, pogué rebre ensenyament superior gràcies a la protecció del duc de Brunsvic, que l’envià a la Universitat de Göttingen Director de l’observatori i professor d’astronomia en aquella ciutat, hi residí fins a la mort, dedicat totalment a una fecunda tasca intellectual Els matemàtics li deuen aportacions transcendentals en la teoria dels nombres i en l’àlgebra noció de congruència i notació corresponent, sistematització de l’ús de demostració rigorosa del teorema fonamental de l’àlgebra, teoria de determinants , etc, qüestions…
discografia
Música
Ciència dedicada a la descripció, l’ordenació i l’estudi de les gravacions sonores.
El terme, però, també es refereix a la relació de discos fonogràfics feta segons la matèria, l’autor o l’intèrpret Es pot aplicar a tota mena d’enregistraments realitzats amb qualsevol mitjà, des del cilindre, el disc o el casset fins als mitjans audiovisuals més sofisticats Una discografia inclou, bàsicament, informació sobre la música, la interpretació i l’enregistrament Les primeres discografies a destacar, la Hot discographie de C Delaunay i The Gramophone Shop Encyclopaedia of Recorded Music, sorgiren cap als anys trenta Bibliografia Complement bibliogràfic Padrol, Jordi Recull de la…
arc
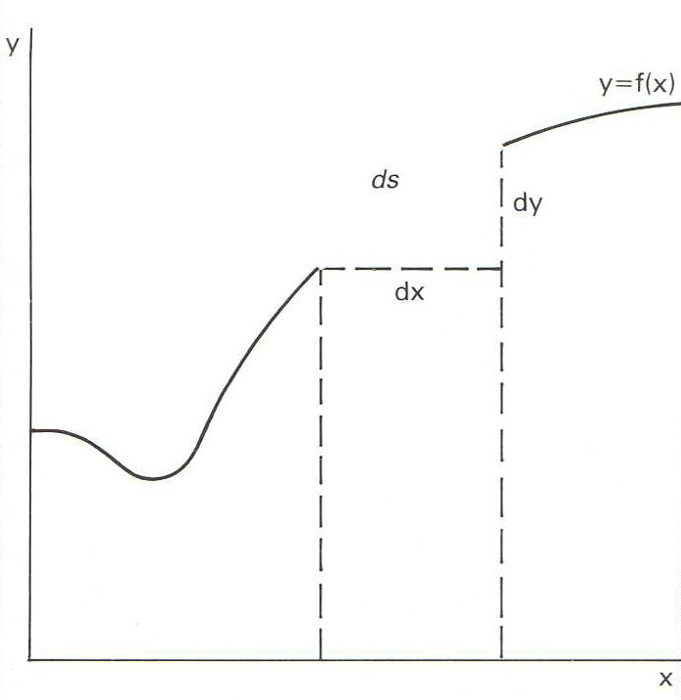
Matemàtiques
Segment o part d’una corba.
Usualment també designa una corba oberta completa Les característiques d’un arc llargada, corda, fletxa depenen de la corba a la qual pertany En el cas d’una circumferència, hom mesura els arcs en unitats d'angle i un arc val igual que l'angle en el centre que el limita en trigonometria, però, hom considera a vegades que un arc de circumferència α, mesurat en radians, admet una infinitat de determinacions que difereixen per un nombre enter de circumferències i són donades per la fórmula α + 2 k π, on k pot ésser zero o un enter qualsevol El principal problema que es planteja a propòsit d’un…
equació diferencial
Matemàtiques
Equació funcional (en el sentit que les incògnites són funcions) on apareixen les derivades de la funció incògnita.
Si la funció és d’una sola variable, l’equació és una equació diferencial ordinària Per tal que aquesta definició, molt general, no inclogui certes classes d’equacions especials com és ara les equacions diferencials en diferències f ´ x = f x + h , hom precisa que la funció incògnita i les seves derivades tan sols poden ésser sotmeses a operacions algèbriques El tipus general d’equació diferencial és escrit F t,x,x´,,x n = 0 Hom defineix l' ordre d’una equació diferencial com el de la màxima derivada que apareix en l’equació Si F té forma polinòmica, hom parla de grau de l’equació…
Leonhard Euler
Matemàtiques
Matemàtic suís.
Deixeble de JBernoulli a la Universitat de Basilea, fou professor de física 1730 i de matemàtiques 1733 a l’Acadèmia de Ciències de Rússia a Peterburg Nomenat, per Frederic el Gran, director de la secció de matemàtiques de l’Acadèmia de Ciències de Berlín, Caterina II el nomenà director de l’Acadèmia de Peterburg 1766 Fou membre de la Royal Society 1746 i de l’Académie Française des Sciences 1755 Estudià les sèries algèbriques i demostrà que només poden ésser emprades quan són convergents Introduí la notació f x , el nombre π, el nombre e com a base de logaritmes, la i per a representar la…
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- …
- Pàgina següent
- Última pàgina