Resultats de la cerca
Es mostren 81 resultats
funció tangent
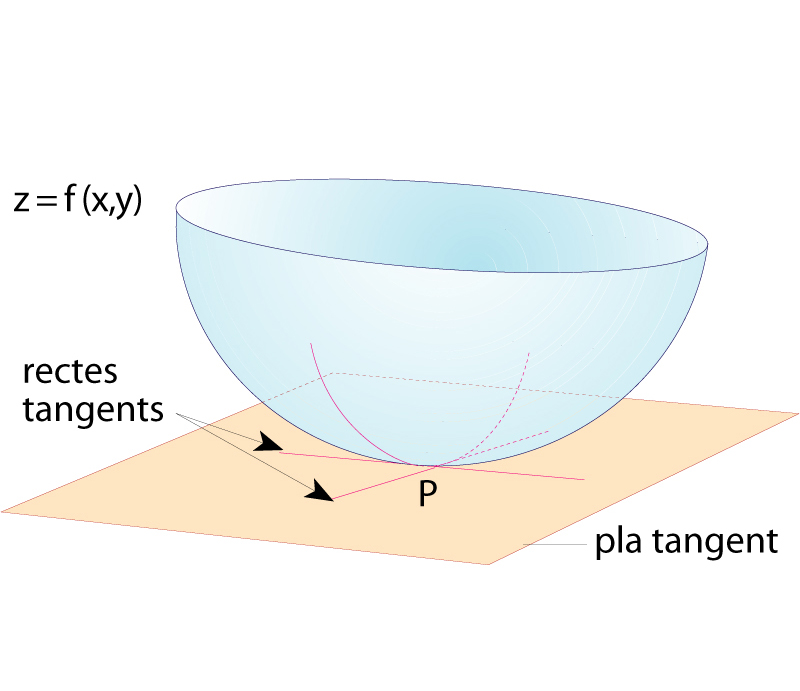
Pla tangent i dues rectes tangents a la superfície z=f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Funció tg: →-{π/2+kπ, k ∈ℤ} →ℝ, definida per l’assignació x
→tg x
, on tg x
és la tangent de l’angle que fa x
radiants.
És una funció periòdica de període 2 i el seu recorregut és -∞, ∞ És una de les sis funcions trigonomètriques o circulars i està relacionada amb les funcions sinus i cosinus per l’expressió tg x =sin x /cos x És indefinidament derivable i el seu desenvolupament en sèrie entera és quan x 2
focènids
Mastologia
Família de mamífers de l’ordre dels cetacis, subordre dels odontocets, molt afí a la dels delfínids i que comprèn els marsuïns.
Són animals relativament petits d’1 a 2 m, de cos més rabassut que el dels dofins, cap de forma cònica, morro poc o molt punxegut i aleta dorsal triangular i poc desenvolupada Són nedadors excellents, habiten en grups nombrosos i són repartits per totes les mars Comprèn tres gèneres i sis espècies Phocaena Ph phocaena , el marsuí comú, Ph spinipinnis, Ph sinus i Ph dioptrica , Phocaenoides Ph dallii i Neophocaena N phocaenoides
funció exponencial complexa
Matemàtiques
Funció f:ℂ→ℂque resulat d’estendre a ℂla funció exponencial.
És anomenada també, simplement, exponencial complexa És definida per l’assignació on z ∈ℂ És periòdica de període 2π i És relacionada amb les funcions trigonomètriques sinus i cosinus per la relació e x + i y = e x cos y + sin y , que permet excriure la forma exponencial d’un nombre complex, z = x + iy = ρ e i ϑ on és el mòdul de z i ϑ = arc tg y/x n'és l’argument
moment d’estabilitat
Física
Transports
Moment del parell d’estabilitat d’un cos i especialment d’una nau que sura.
Les dues forces d’aquest parell són el desplaçament, que actua de dalt a baix sobre el centre de gravetat, i la resultant de les pressions que exerceix l’aigua sobre el buc, que actua de baix a dalt i hom considera que ho fa sobre el centre de pressió El moment d’estabilitat és el producte del desplaçament pel braç del parell, i el braç del parell equival al producte de l’altura metacèntrica pel sinus de l’escora
condició d’aplanetisme d’Abbe
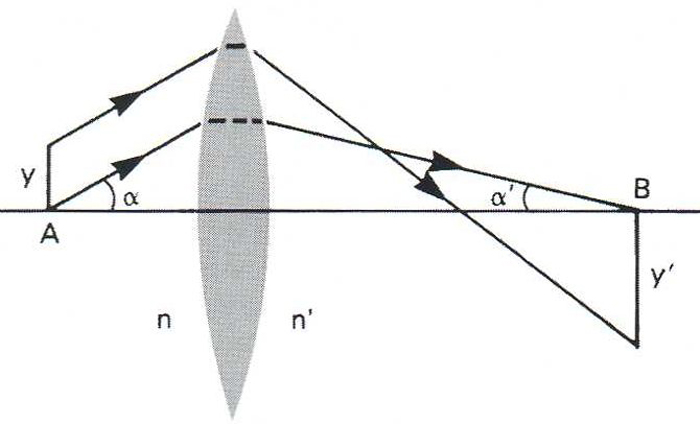
Condició d’aplanetisme d’Abbe. A punt objecte; B punt imatge; y objecte; y' imatge; α angle objecte; α' angle imatge
© fototeca.cat
Física
Relació que ha de complir un sistema òptic perquè sigui aplanètic.
L’expressió que la dóna és n y sinα = n'y' sinα’, essent n i n' els índexs de refracció del medi objecte i imatge, i y i y' les dimensions transversals d’objecte i imatge, i α i α’ els angles que forma una mateix raig que havent sortit del punt objecte A arribi al punt imatge B Un sistema és aplanètic si verifica aquesta condició per a qualsevol punt de l’eix i unes certes dimensions transversals És anomenada també condició del sinus
tangent d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i una circumferència de radi unitat centrada en el punt d’intersecció dels eixos (cercle goniomètric), i un segment que forma un angle α amb l’eix d’abcisses x, longitud del segment, perpendicular a l’eix d’abcisses, deteminat entre el punt de la circumferència de coordenades (1,0) i el punt en què aquest segment s’interseca amb el segment inclinat l’angle α en qüestió.
Aquesta longitud és la tangent de l’angle α, i és denotada per tgα És vàlida la següent igualtat tgα=sin α/cos α, on sin és el sinus d’un angle i cos és el cosinus d’un angle La tangent de l’angle α determinat entre dos segments qualssevol és la tangent de l’angle que, dibuixat sobre el cercle goniomètric, té la mateixa obertura que α Algunes fòrmules trigonomètriques relatives a la tangent d’un angle són tgα+β=tgα+tgβ/1-tgα- tgβ tg-α=-tgα tgα+tgβ- =sinα+β/cosα cosβ
funció cosinus
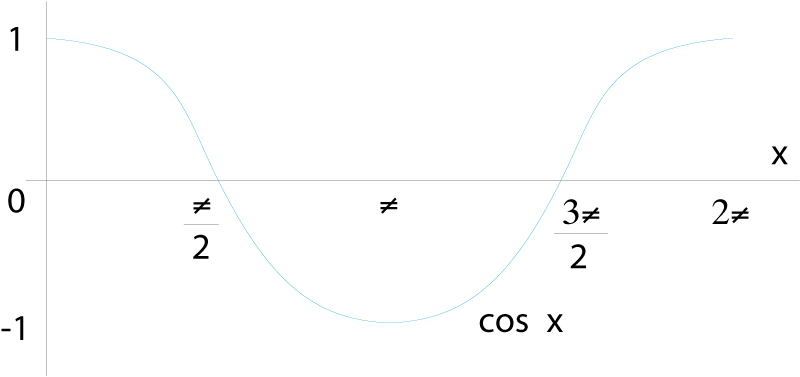
Representació gràfica de la funció y=cos x
© Fototeca.cat
Matemàtiques
Funció cos: ℝ→ℝdefinida per l’assignació x →cos (x), on cos(x) és el cosinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1, 1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció sinus per la derivada dcos x/ dx = -sin x, dsin x/ dx = cos x És indefinidament derivable, i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió cos x=e i x + e - i x /2, relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció cosinus complex
producte vectorial de dos vectors
Matemàtiques
Operació definida entre dos vectors.
Donats dos vectors, a i b , vector a ∧ b el mòdul del qual és | a ∧ b | = | a | | b | sin a , b , on sin a , b és el sinus de l’angle que determinen les direccions de a b , i la direcció del qual és perpendicular al pla determinat per a i b , i el sentit del qual és tal que el tríedre a , b , a ∧ b sigui dextrogir és a dir, que el sentit de a ∧ b és igual al sentit d’avanç d’un llevataps que, aplicat en el punt de concurrència de a i b , anés del primer cap al segon
cosinus d’un angle
Matemàtiques
Donats dos eixos perpendiculars x
i y
, i un segment de longitud unitat OP
que forma un angle α amb l’eix d’abscisses x
, valor de la projecció de OP
sobre l’eix x
.
Aquesta projecció és el cosinus de l’angle α i és denotada per cos α El cosinus de l’angle α determinat entre dos segments qualsevol és el cosinus de l’angle que, dibuixat sobre aquest cercle goniomètric, té la mateixa obertura que α Algunes fórmules trigonomètriques relatives al cosinus d’un angle són cosα+β=cosα cosβ-sinα sinβ cos-α= cosα cosαcosβ = cosα+β+cosα-β/2 cosα + cosβ = 2 cosα + β/2cosα - β/2 Entre el cosinus i el sinus d’un angle hi ha la relació fonamental cos 2 α + sin 2 α = 1