Resultats de la cerca
Es mostren 218 resultats
autovector
Matemàtiques
En un endomorfisme d’un espai vectorial, qualsevol dels vectors no nuls sobre els quals l’endomorfisme actua com a homotècia.
Són vectors v no nuls tals que per a l’endomorfisme f satisfan la condició f v = λ v per a un cert nombre λ, dit autovalor o valor propi associat a v
gràfic vectorial escalable

Dibuix d’una poma en format SVG
Electrònica i informàtica
Format de fitxer XML per a descriure gràfics vectorials de dues dimensions, tant estàtics com dinàmics.
versor
Matemàtiques
Vector de norma unitat.
És anomenat també vector unitari Si e és un vector nul d’un espai vectorial normat E , ∥ ∥, el vector 1/∥ e ∥ e és un versor El procés que converteix e en 1/∥ e ∥ e és anomenat normalització Els versors de ℝ 3 són notats per i , j i K
translació
Matemàtiques
Transformació geomètrica que a cada punt M
del pla n’hi associa un altre M’
de manera que el vector de manera que el vector
sigui un representant d’un vector lliure
prefixat, anomenat vector de la translació
Les translacions són isometries que en el pla conserven el sentit de les rotacions i en l’espai el caràcter dels tríedres, no tenen punts dobles i en les quals les rectes i els plans parallels al vector de translació són invariants El conjunt de totes les translacions del pla o de l’espai formen un grup commutatiu amb l’operació composició, el qual és isomorf al grup additiu dels vectors lliures ordinaris associats al pla o a l’espai considerat Si és el vector característic d’una translació, el punt transformat d’un punt M x 1 ,x 2 ,x 3 és el punt M' x' 1 ,x' 2 ,x'…
norma
Matemàtiques
En els espais vectorials de dimensió 1, 2 o 3 (recta, pla, espai ordinari), longitud d’un vector.
Si el vector és determinat per les seves components en un sistema de coordenades ortonormals eixos perpendiculars i unitats iguals sobre cada eix, la norma del vector v = x 1 , x 2 , x 3 és expressada així Per mitjà del producte escalar, és D’aquesta manera la noció de norma s’estén a espais vectorials de dimensió qualsevol, finita o infinita La norma té en tot cas les propietats de la distància, és a dir, és positiva o nulla, només el vector zero té norma nulla, i satisfà la desigualtat triangular,
polarització
Física
Condició d’una radiació lluminosa (o, en general, electromagnètica) el vector del camp elèctric de la qual manté una certa orientació.
Si en tots els punts de la direcció de propagació el dit vector roman sempre en un mateix pla pla de polarització , hom diu que la polarització és plana o lineal Si en cada punt de la direcció de propagació el dit vector descriu, en el decurs del temps, una circumferència, hom diu que la polarització és circular , i si descriu una ellipse hom diu que la polarització és ellíptica
lliscador
Matemàtiques
Parell (D,v) format per una recta D d’un espai afí, anomenada suport (del lliscador), i per un vector v de la mateixa direcció, pertanyent a l’espai vectorial associat.
És anomenat també vector lliscant
regla de l’observador d’Ampère
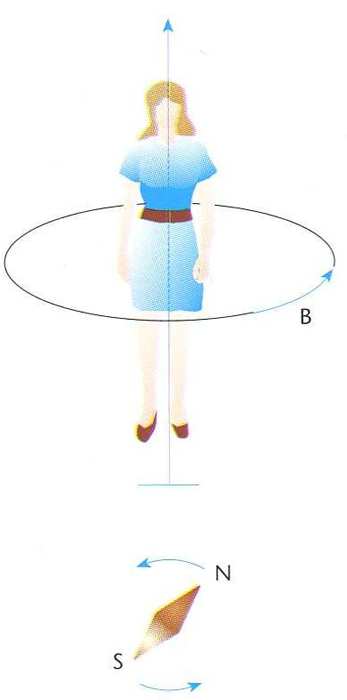
La regla de l’observador d’Ampère permet recordar l’efecte d’un corrent elèctric sobre un imant
© Fototeca.cat
Electrònica i informàtica
Regla que permet de recordar el sentit del vector d’inducció magnètica B produïda en un punt prop d’un corrent que circula per un conductor rectilini i indefinit.
Pressuposa un observador imaginari tal que, travessat de peus a cap pel corrent, veu en el punt considerat el vector B en el sentit de dreta a esquerra
base d’un espai vectorial
Matemàtiques
Conjunt de vectors linealment independents que generen l’espai vectorial mitjançant combinacions lineals, és a dir, tals que qualsevol vector v de l’espai pot ésser expressat d’una manera unívoca com a combinació lineal dels vectors de la base:
Les coordenades a 1 ,, a n de v en la base e 1 ,, e n són úniques Tot espai vectorial té una base és una conseqüència de l’axioma de Zermelo Si l’espai E té una base formada per un nombre finit d’elements base finita l’espai és de dimensió finita aleshores totes les bases tenen el mateix nombre d’elements, nombre que s’anomena la dimensió de l’espai , dim E Un espai vectorial de dimensió finita té infinites bases Dues bases de E , B = e 1 ,, e n i B’ = e’ 1 ,, e’ n es relacionen mitjançant una matriu de canvi de base essent és a dir, les matrius A i B són inverses B = A -1 La matriu…
fórmules de Fresnel
Física
Fórmules que relacionen les amplituds reflectida (A´´) i refractada (A´) amb l’amplitud incident (A) del camp elèctric d’una ona lluminosa que incideix sobre un dielèctric isòtrop.
En el cas que el vector del camp elèctric sigui parallel al pla d’incidència, les fórmules són i essent l’angle d’incidència i r l’angle de refracció, i en el cas que el vector sigui perpendicular són En el cas que tingui una direcció qualsevol, per descomposició del vector aquest cas és reduït als anteriors Les fórmules de Fresnel permeten també d’estudiar el canvi de fase entre les ones incident, reflectida i refractada