Resultats de la cerca
Es mostren 5896 resultats
convolució
Matemàtiques
Donades dues funcions reals de variable real, f(x) i g(x), funció definida per la integral: .
La convolució, o producte de convolució , té les propietats commutativa, associativa i distributiva Hi ha dos teoremes importants sobre la convolució El primer, o teorema de Parseval , afirma que la transformada de Laplace o de Fourier de la convolució de dues funcions és el producte de les transformades de Laplace o Fourier, respectivament, de les dues funcions Ff*g y = Ff y x Fg y Segons el segon, la transformada de Fourier del producte de dues funcions és igual a la convolució de les seves transformades dividit per 2π Ff x g y…
funció negligible respecte a una funció en un punt
Matemàtiques
Donada una funció g:D ⊂ℝ→ℝi un punt a adherent a D, funció f:D ⊂ℝ→ℝ.
Per a tot ε > 0, existeix un entorn U de a tal que ¦ f x ¦≤ε¦ g x ¦ per a tot x ∈ U ∩ D Hom diu que f és negligible respecte a g en a o que f és dominada per g en a , o que g és preponderant sobre f en a
Ferran Soriano i Rivero
Ferran Soriano i Rivero
© Arxiu F. Soriano
Escultura
Literatura catalana
Escultor.
S’inicià de jove en el modelatge de l’acer, i aviat incorporà aquest material a l’expressió artística Es formà a París 1974 i a Roma 1975 en la tècnica de l’escultura, i amb el gravador Josep Badia en la tècnica del gravat Installat des de fa cinquanta anys a l’Hospitalet de Llobregat, té, des de fa més de trenta, estudi a Sant Boi de Llobregat La seva obra, de caràcter simbolista, es troba situada en espais públics de l’Hospitalet de Llobregat, ciutat amb cinc obres escultòriques seves, entre les quals hi ha la cèlebre Vol de coloms , Sant Boi de Llobregat, Begues, Sant Pere de Ribes i…
Flavi Avià
Literatura
Escriptor llatí del final del segle IV dC.
És conegut com a autor de quaranta-dues faules en versos elegíacs, escrites en un llatí decadent, que tingueren gran difusió a l’edat mitjana
derivada parcial d’una funció en un punt
Matemàtiques
Donada una funció real, f:D⊂ℝn→ℝ, i un punt del seu domini de definició, a=(a1,...,an) ∈D, derivada en el punt ai de les funcions d’una variable fi(xi) = f(a1,...,xi,...,an)
.
La i-èsima derivada parcial de f en el punt a és, doncs, el nombre ∂ f/∂x i a = df i /dx i a i Si aquesta és, al seu torn, derivable, hom pot definir derivades parcials d’ordres superiors , com, per exemple, ∂ 2 f /∂ x i ∂x j = ∂∂ f / ∂x i / ∂ x j
ordre d’una derivada
Matemàtiques
Respecte a una funció original, f, nombre de derivacions que hom ha fet fins a arribar a la derivada en qüestió.
Si f n és la derivada d’ordre n , o derivada n-èsima , de la funció f , se satisfà que f n = f n-1 '
axioma de l’elecció
Matemàtiques
Axioma que admet que, donat un conjunt A, existeix una aplicació f del conjunt dels subconjunts no buits de A en A tal que f(B) pertany a B per a tot B de A diferent del buit.
D’una manera informal, l’aplicació f escull un element de cada subconjunt no buit de A Cal fer notar que no és un axioma constructiu, en el sentit que no es té cap indicació sobre la manera de construir una tal f L’axioma de l’elecció equival a la possibilitat de dotar qualsevol conjunt d’una bona ordenació teorema de la bona ordenació L’axioma de l’elecció és equivalent al lema de Zorn
funció imparella
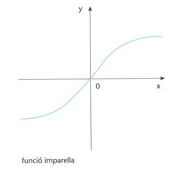
Funció imparella
© Fototeca.cat
funció parella
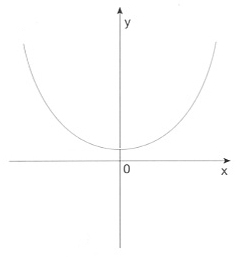
funció parella
ordre d’una derivada parcial
Matemàtiques
Respecte a una funció original, f, nombre de derivacions parcials que hom ha fet fins a arribar a la derivada en qüestió.
Per exemple, les derivades parcials de ∂ f /∂ x i són les derivades parcials d’ordre 2 , o de segon ordre , de f , i són notades per ∂ 2 f /∂ x j ∂ x i on j = 1, , n
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- …
- Pàgina següent
- Última pàgina