Resultats de la cerca
Es mostren 5882 resultats
ombra
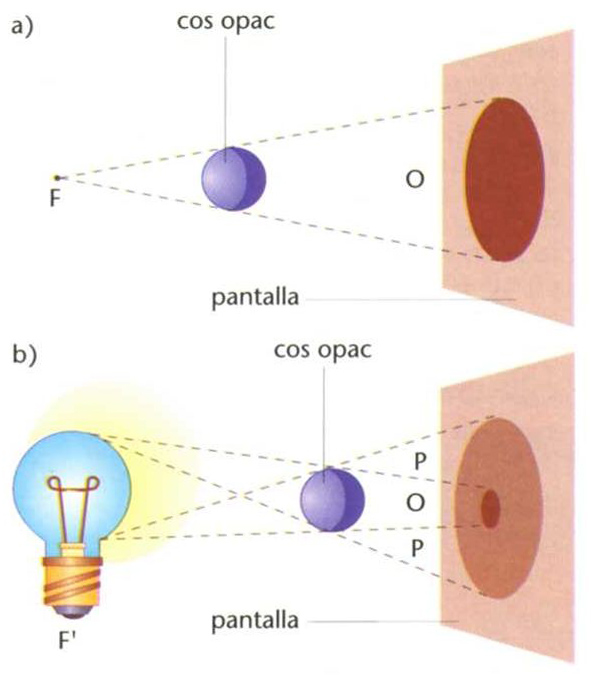
Ombra: 1, ombra O produïda per la font lluminosa puntual F1; 2, ombra P produïda per la font lluminosa extensa F2. La regió O és la pròpiament anomenada ombra; la regió P és la penombra
© Fototeca.cat
Imatge que hom recull sobre una pantalla que reprodueix en silueta la forma d’un cos opac situat entre la font lluminosa i la pantalla.
efecte Doppler
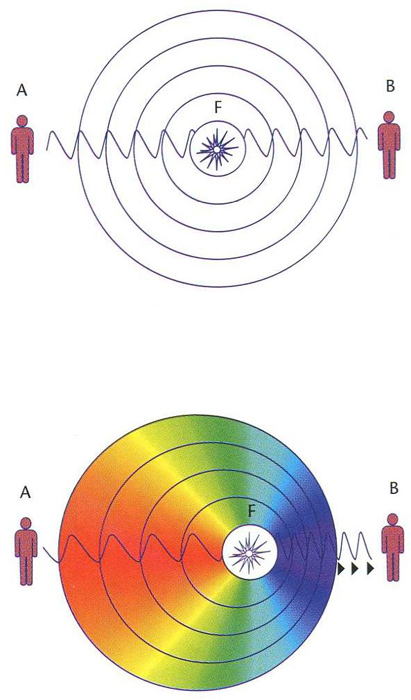
Si la font F no es mou, la freqüència de les ones és la mateixa per a A i B (a dalt); si F s’allunya de A i s’acosta a B, hi ha un desplaçament cap al vermell per a A i cap al violeta per a B (a baix)
© Fototeca.cat
Física
Donada una font que emet una ona (sonora, electromagnètica, etc), diferència entre la longitud d’ona emesa i la longitud d’ona que percep un observador, causada pel moviment relatiu entre font i observador.
Descobert per Doppler el 1842, fou descobert independentment per Fizeau el 1848, per la qual cosa és anomenat també efecte Doppler-Fizeau En el cas del so, l’efecte es tradueix en l’augment del to cap als aguts en aproximar-se la font a l’observador i en la disminució cap als greus en allunyar-se'n per exemple, és el cas del xiulet de la locomotora En el cas de la llum, el moviment d’aproximació entre la font lluminosa i el receptor produeix un desplaçament de les ratlles de l’espectre cap al violeta, mentre que un allunyament de la font en provoca un desplaçament cap al vermell A escala…
funció reglada
Matemàtiques
Funció f:[a,b]⊂ℝ→ℝtal que admet un límit a l’esquerra en tot punt de l’interval (a,b] i un límit a la dreta a tot punt de l’interval [a,b)
.
Hom diu aleshores que f és reglada sobre l’interval a,b Una funció f és reglada sobre a,b si i només si és el límit uniforme d’una successió de funcions esglaonades en a,b
homeomorfisme
Matemàtiques
Aplicació biunívoca f entre dos espais topològics tal que f i la seva inversa f - 1 són contínues.
força de Coriolis
Física
Força fictícia F C , similar a la d’inèrcia que apareix en aplicar la segona llei de Newton als sistemes de referència que giren respecte als sistemes inercials.
Els seu valor és donat per la fórmula F C = m a C , on l’acceleració de Coriolis acceleració de Coriolis
funció homogràfica
Matemàtiques
Funció f:ℂ→ℂdefinida per f(z)=(az+b)/(cz+d) quan z≠∞ i z≠-d/c, i per f(∞)=a/c i f(-d/c)=∞.
Quan ad - bc ≠0 hom parla de funció homogràfica pròpia , i quan ad - bc =0 de funció homogràfica impròpia
proposició
Lògica
En la lògica simbòlica, sentència l’esquema quantificacional atòmic de la qual inclou lletres predicats (‘F’, ‘G’, ‘H’; corresponents al verb o predicat verbal) i lletres arguments (‘w’, ‘x’, ‘y’, ‘z’; corresponents al subjecte).
En l’esquema logístic, doncs, hom prescindeix de la representació tradicional de proposició segons la qual aquesta consta d’un subjecte i un predicat units per la còpula ‘és’, que no és reconeguda sinó com una de les moltes formes possibles de proposició, i hom estableix, en canvi, que en les proposicions dividides per l’atomisme lògic en atòmiques i compostes un predicat és afirmat d’un argument Representacions quantificacionals de proposicions atòmiques són, per exemple, ‘Fx', on ‘x’ substitueix ‘Pere’, ‘F’ substitueix ‘corre’ o ‘és bo’, etc, i ‘Fx,y' o ‘Fx' segons que F…
funció de variació fitada
Matemàtiques
Funció f
:[ a,b
]⊂ℝ→ℝtal que existeix un nombre real M
>0 tal que per a tota subdivisió de l’interval de definició, a
=
x 0
<
x 1
<...<
x n
= b
, se satisfà que la suma
.
El menor nombre M que satisfà aquesta condició és anomenat variació total de f sobre a,b
subespai
Matemàtiques
Qualsevol subconjunt no buit F d’un espai vectorial E (sobre un cos K) tal, que és estable per a les dues lleis de E i que, proveït d’aquestes lleis induïdes, és també un espai vectorial (sobre K).
En l’espai vectorial de tres dimensions ℝ 3 els subespais són el mateix espai, l’origen de coordenades i totes les rectes i els plans que passen per l’origen F és un subespai de E si, donats qualssevol x , y de F i λ de K , aleshores la combinació lineal x ,-λ y pertany a F Tota família de vectors determina l’anomenada envolupant lineal , o mínim subespai, que els conté La intersecció M ∩ N de dos subespais M i N és un subespai, però la reunió M ∪ N no ho és en general La suma M + N definida per a tots els vectors que són suma d’un element de M i un de…