Resultats de la cerca
Es mostren 278 resultats
Heró d’Alexandria
Matemàtiques
Matemàtic i inventor grec.
Establí una fórmula per a obtenir l’àrea d’un triangle sabent les longituds dels costats i un mètode aproximatiu per a calcular les arrels quadrades i cúbiques Trobà solucions algèbriques de les equacions de primer i segon grau i resolgué per mètodes aritmètics algunes equacions quadràtiques
Charles Émile Picard
Matemàtiques
Matemàtic francès.
Professor a París, estudià les funcions analítiques uniformes i les equacions diferencials lineals amb coeficients periòdics Ideà un mètode d’aproximacions successives per a resoldre equacions diferencials Estudià analíticament les funcions algèbriques i llurs integrals Publicà, entre altres obres, Traité d’analyse 1891-95, en tres volums, i Equations fonctionnelles 1929
Paolo Ruffini
Matemàtiques
Matemàtic i metge italià.
Fou professor a Mòdena Estudià principalment les equacions algèbriques i demostrà la no-solució algèbrica de les equacions de cinquè grau o superiors Publicà Teoria Generale dell’equazione 1799, Memoria sul tifo contagioso i d’altres obres posteriors N'ha estat publicada també l’obra Opere matematiche 1915-54, en 3 volums
Alexandre Vandermonde
Matemàtiques
Matemàtic francès.
Estudià les equacions cúbiques i quadràtiques i d’altres, com la del tipus x n -1 = 0 per a tot n nombre primer Amb Lagrange elaborà mètodes per a resoldre equacions 1771, i són especialment importants els estudis sobre els determinants 1772 S'ocupà també de la mecànica i de l’acer
superfície
Matemàtiques
Conjunt de punts de l’espai que poden ésser determinats per dos paràmetres.
La manera més simple de determinar una superfície és donar una o més equacions del tipus z = f x,y Elegit un punt x,y en el domini de definició de la funció f , aquesta funció o aquestes funcions donen els valors de z , que, juntament amb x,y , són les coordenades cartesianes dels punts de la superfície Les funcions que donen la superfície esfèrica són , on el signe + correspon a l’hemisferi superior, i el signe - a l’hemisferi inferior L’equació z = ax + by + c correspon al pla o superfície plana Sovint és difícil, o impossible, d’expressar una superfície per mitjà de les…
Ars magna
Matemàtiques
Tractat d’àlgebra de Gerolamo Cardano editat a Nuremberg el 1545.
Representa el primer intent de teoria sistemàtica d’equacions, i inclou alguns càlculs amb nombres negatius, bé que ell mateix no els admetia També conté els treballs posteriors del seu deixeble Ludovico Ferrari, amb l’estudi de les equacions de quart grau i llurs solucions L’aparició d’aquesta obra inicià la controvèrsia entre Tartaglia i Cardano
hamiltonià
Tecnologia
En un sistema dinàmic amb n
graus de llibertat, funció donada per l’expressió
.
, on Lt,q 1 ,,q n ,p 1 ,,p n és el lagrangià del sistema, les q i són les coordenades generalitzades, les p i els corresponents moments canònics p i =∂ L /∂ q i , i t és el temps El hamiltonià representa l’energia total del sistema, és a dir, la suma de les energies cinètica i potencial Hom en deriva les equacions canòniques del moviment o equacions de Hamilton
girador
Electrònica i informàtica
Tecnologia
Convertidor d’energia que, tot mantenint la forma d’energia, canvia la variable extensiva
T 1
de l’entrada en la variable intensiva
A 2
de la sortida, i viceversa.
El girador ideal és definit per les equacions A 2 = r g T 1 on r g rep del nom de de raó de girament El girador elèctric és un quadripol passiu caracteritzat per les equacions v 2 = r g i 1 v 2 = - r g v 1 on r g té les dimensions d’una resistència elèctrica la seva aplicació més important és la simulació d’inductors per mitjà de condensadors
anàlisi funcional
Matemàtiques
Estudi d’espais vectorials topològics els elements dls quals són funcions.
Els espais funcionals més interessants són els de les funcions contínues, el de les funcions integrables i el de les funcions normades Els principals conceptes de l’anàlisi, com la diferenciació i la integració, es poden generalitzar a espais de Banach donant lloc a estudis típics d’anàlisi funcional Té importants aplicacions a l’estudi d’equacions diferencials en derivades parcials, equacions funcionals i integrals, usant teoremes generals com el de Hahn-Banach, el de Riesz o el de l’apliació oberta
bisectriu
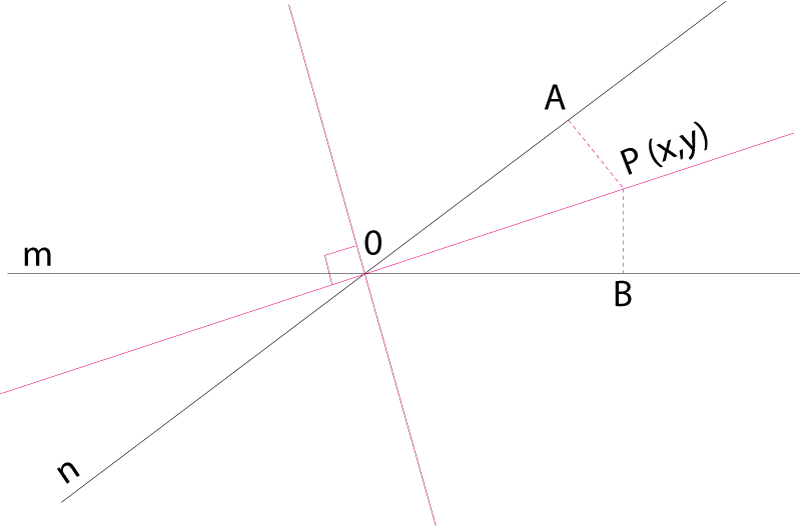
Bisectrius corresponents als quatre angles determinats per dues rectes que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels costats d’un angle, el qual divideix, per tant, en dos angles iguals.
Dues rectes que es tallen determinen quatre angles, iguals dos a dos Llurs bisectrius són dues rectes perpendiculars entre elles En considerar un dels quatre angles hom distingeix la bisectriu interior i la bisectriu exterior Les equacions de les bisectrius dels angles que determinen dues rectes que es tallen, les d’equacions de les quals són, en una referència cartesiana normal, A 1 x + B 1 y + C 1 = 0 i A 2 x + B 2 y + C 2 =0, són