Resultats de la cerca
Es mostren 65 resultats
el·líptic | el·líptica
el·líptic | el·líptica
paraboloide el·líptic
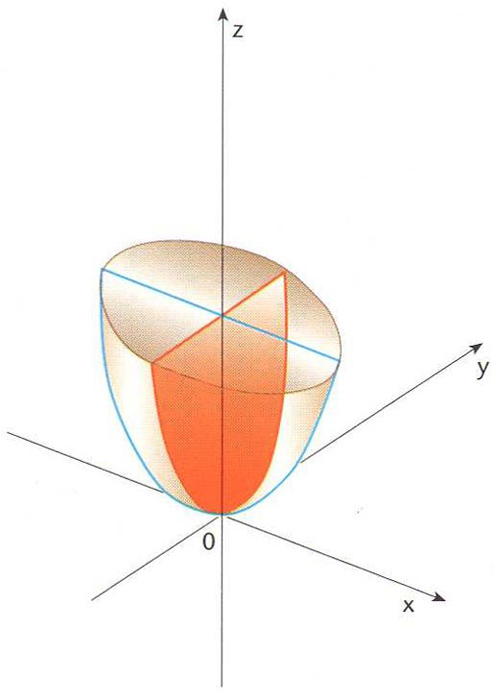
Paraboloide el·líptic on hi ha traçada una el·lipse i una paràbola
© Fototeca.cat
Matemàtiques
Paraboloide d’equació
x 2
/a 2
+
y 2
/b 2
= 2 z
, on a
i b
són constants.
La seva intersecció amb un pla que contingui l’eix de simetria és una paràbola, mentre que la intersecció amb un pla perpendicular a l’anterior dóna una ellipse
el·lipsògraf
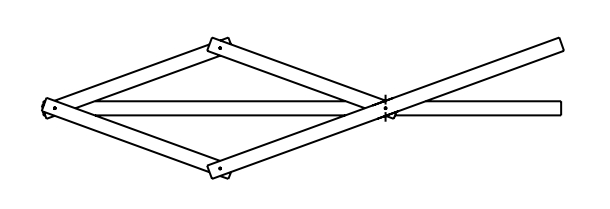
El·lipsògraf de quadrants
cilindre
Matemàtiques
Cos reglat generat per una corba plana (directriu) que estrasllada segons una direcció no paral·lela al pla de la corba.
Així, es parla de cilindre ellíptic , hiperbòlic , parabòlic , etc per a indicar la corba directriu
ditisc
Entomologia
Insecte de l’ordre dels coleòpters, de la família dels ditíscids, de grans dimensions i adaptat a la vida aquàtica.
Té el cos ellíptic i aplanat, amb les potes en forma de rems, proveïdes de sedes natatòries S'alimenten de batracis i peixos petits L’espècie més abundant als Països Catalans és Dytiscus marginalis
punt umbilical
Matemàtiques
Punt d’una superfície per al qual la recta normal a ella és aresta d’un feix de plans, els quals tallen la dita superfície segons corbes que tenen, en aquest punt, el mateix radi de curvatura.
En la superfície esfèrica, tots els punts són umbilicals Si tots els radis de curvatura tenen el mateix sentit, el punt és anomenat ellíptic , mentre que si hi ha curvatures de sentits diferents el punt és hiperbòlic En els punts umbilicals, cada recta tangent a la superfície és perpendicular a la seva conjugada
hiperboloide
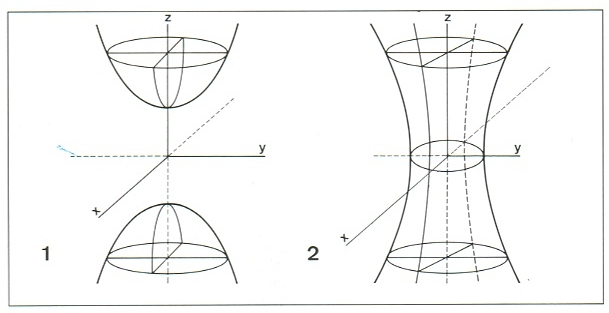
hiperboloide 1, de dues fulles; 2, d'una fulla
Matemàtiques
Quàdrica que, respecte als seus tres eixos de simetria, té per equació (x2/a2) + (y2/b2) - (z2/c2) = ±1.
Entre les seves seccions planes, n'hi ha que són hipèrboles Quan el signe del segon membre és +, l’hiperboloide és anomenat d’una fulla o hiperbòlic quan és -, l’hiperboloide és anomenat de dues fulles o ellíptic Un hiperboloide és anomenat de revolució quan hom el pot considerar generat per la rotació d’una hipèrbola entorn d’un dels seus eixos de simetria