Resultats de la cerca
Es mostren 13 resultats
hamiltonià
Física
Operador sobre l’espai de Hilbert d’un sistema físic descrit per la mecànica quàntica, que representa l’energia observable.
Pot ésser obtingut del hamiltonià del corresponent sistema clàssic substituint coordenades i moments pels corresponents operadors Els seus valors propis són els valors possibles de l’energia espectre d’energies i els vectors propis són els estats estacionaris Incorpora la dinàmica concreta del sistema en l’equació de Schrödinger , on |ψ t > és un estat del sistema ket i h és la constant reduïda de Planck
hamiltonià
Tecnologia
En un sistema dinàmic amb n
graus de llibertat, funció donada per l’expressió
.
, on Lt,q 1 ,,q n ,p 1 ,,p n és el lagrangià del sistema, les q i són les coordenades generalitzades, les p i els corresponents moments canònics p i =∂ L /∂ q i , i t és el temps El hamiltonià representa l’energia total del sistema, és a dir, la suma de les energies cinètica i potencial Hom en deriva les equacions canòniques del moviment o equacions de Hamilton
mecànica analítica
Tecnologia
Part de la mecànica racional que comença amb la magistral obra de Joseph-Louis Lagrange Mécanique analytique (1788) i continua amb les obres de W.R.Hamilton (1834) i C.G.Jacobi (1842).
Gràcies al progrés que havia experimentat l’anàlisi infinitesimal, Lagrange reduí al mínim els postulats de la dinàmica i en deduí, per mitjà del càlcul diferencial i del càlcul integral, unes fórmules generals, anomenades equacions de Lagrange, aplicables a tota mena de problemes mecànics concrets, en les quals l’energia cinètica té un paper principal Encara actualment les equacions de Lagrange són aplicades correntment, sobretot als sistemes de sòlids, com ara als d’oscilladors mecànics o elèctrics, i també als de corpuscles microfísics WRHamilton elaborà primerament una òptica matemàtica…
graf de Petersen
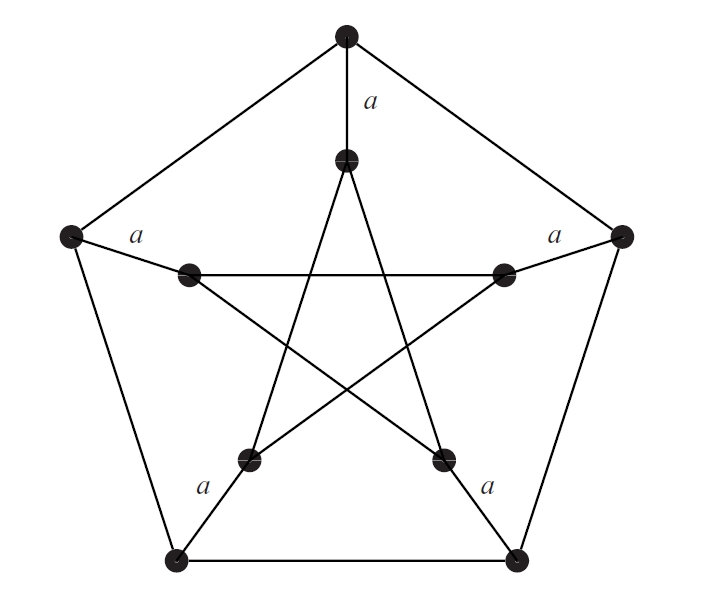
graf de Petersen
Matemàtiques
Graf 3-regular, d’ordre 10, que té diàmetre 2.
A més, és el graf 3-regular de diàmetre 2 amb el nombre més gran de vèrtexs El graf de Petersen és un graf vèrtex-transitiu amb nombre cromàtic 4, que no és de Cayley ni hamiltonià
integral de ressonància
Química
Integral definida en l’estudi mecanicoquàntic de l’estructura molecular.
La integral queda definida per β = ∫φ 1 Hφ 2 d τ = ∫φ 2 Hφ 1 d τ essent φ 1 i φ 2 dos orbitals atòmics diferents, i H l’hamiltonià del sistemaÉs un dels components de l’energia electrònica en l’estudi d’aquesta pel mètode dels orbitals moleculars El seu valor és sempre negatiu, i el seu significat físic és el d’una estabilització addicional del sistema a causa de la deslocalització d’un parell electrònic entre els orbitals atòmics φ 1 i φ 2
funció de Routh
Física
Per a un sistema de n graus de llibertat, funció donada per la fórmula .
on s i t són enters tals que s + t = n , les q i amb i variant d’1 a s són les coordenades generalitzades que tenen com a moments lineals les p i , les ξ j amb j variant d’1 a t són les coordenades generalitzades per a les quals, pel fet de no tenir un moment lineal fàcilment utilitzable, hom prefereix emprar les coordenades de velocitat generalitzades x j , i L és la funció de Lagrange del sistema Respecte a les coordenades q i , la funció de Routh és anàloga al hamiltonià i respecte a les ξ j , ho és al lagrangià Per tant La funció de Routh simplifica el problema que té…
model atòmic de Schrödinger
Física
Química
Model derivat de l’aplicació de l’equació de Schrödinger (Hψ = Eψ) per a l’estudi de l’estructura atòmica.
Per a un sistema determinat, les diferents funcions pròpies ψ, solucions de l’equació, són conegudes com a orbitals orbital , i són caracteritzades per uns valors propis que corresponen a l’energia dels esmentats orbitals El mòdul al quadrat de la funció ψ té el significat de la probabilitat de localització de l’electró que descriu l’esmentada funció en una regió determinada de l’espai, i la seva representació gràfica constitueix la imatge visual dels orbitals, habitualment emprada pels químics El coneixement exacte del hamiltonià H pot ésser únicament assolit en els sistemes…
principi de causalitat
Física
Principi segons el qual el coneixement de les condicions inicials d’un sistema físic en un instant t0 i de la dinàmica que el controla (forces i equació del moviment) determinen completament els valors de les variables dinàmiques en tot temps t posterior a t0.
En el marc de la dinàmica clàssica, aquest determinisme és palesat pel fet que l’equació diferencial del moviment té una solució única un cop especificades les condicions inicials El sorgiment de la relativitat i de la mecànica quàntica modificaren aquesta concepció En el context relativista, el principi de causalitat consisteix en l’afirmació que un esdeveniment no pot precedir les seves conseqüències això es tradueix en una exigència a l’hora de relacionar dinàmicament dos esdeveniments —l’ordenació temporal dels quals depèn generalment del sistema de referència des del qual l’observador…