Resultats de la cerca
Es mostren 174 resultats
Anàlisi de vectors (Gibss)
Anàlisi de vectors Gibss
sistema lliure de vectors
Matemàtiques
Sistema no lligat de vectors, format consegüentment per una família de vectors linealment independents (dependència lineal).
sistema lligat de vectors
Matemàtiques
Qualsevol conjunt de vectors linealment dependents (dependència lineal).
producte vectorial de dos vectors
Matemàtiques
Operació definida entre dos vectors.
Donats dos vectors, a i b , vector a ∧ b el mòdul del qual és | a ∧ b | = | a | | b | sin a , b , on sin a , b és el sinus de l’angle que determinen les direccions de a b , i la direcció del qual és perpendicular al pla determinat per a i b , i el sentit del qual és tal que el tríedre a , b , a ∧ b sigui dextrogir és a dir, que el sentit de a ∧ b és igual al sentit d’avanç d’un llevataps que, aplicat en el punt de concurrència de a i b , anés del primer cap al segon
producte escalar de dos vectors
Matemàtiques
Donats dos vectors a i b, nombre real a·b definit com el producte dels mòduls de a i b pel cosinus de l’angle que determinen: a·b = |a| |b| cos (a,b)
.
resultant
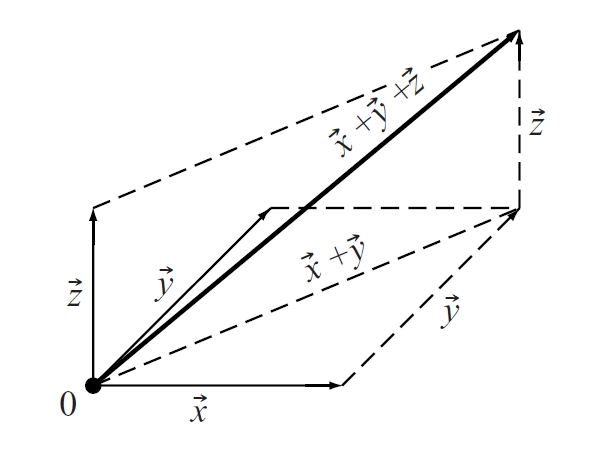
Resultant d’una suma de vectors
Física
Vector equivalent a la suma de dos vectors.
Donats dos vectors, hom n'obté la resultant per la regla del parallelogram cal construir un parallelogram que tingui per costats els vectors donats, i la resultant és aleshores la diagonal d’aquest parallelogram
equipol·lència
Matemàtiques
Relació d’equivalència entre vectors fixos de l’espai euclidià.
Dos vectors són equipollents si existeix una translació que transforma l’un en l’altre Les classes de vectors equipollents són anomenades vectors lliures vector
tríedre de Frenet
Matemàtiques
Tríedre trirectangle constituït pels vectors tangent, normal i binormal a una corba en un punt.
Donada una corba C , parametritzada per l’abscissa curvilínia s s dona la longitud de l’arc des d’un punt de referència de la corba, C s = x s , y s , z s , tríede ortonormal directe definit en cada punt P de C pels vectors tangent t , normal n i binormal b , l’expressió dels quals és t = d C s / ds P , ∥ t ∥=1 n = d t / ds /∥ d t / ds ∥ P , ∥ n ∥=1 b = t ∧ n , ∥ b ∥=1 El pla P , t , n és el pla osculador de la corba C en el punt P , el pla P , n , b és el pla normal de C en P , i el pla P , b , t és el pla rectificador de C en P El radi de curvatura de C és R s =…
determinant de Gram
Matemàtiques
Determinant de la matriu de Gram de n vectors donats d’un espai vectorial dotat d’un producte escalar.
És no nul si, i solament si, els vectors són linealment independents
base d’un espai vectorial
Matemàtiques
Conjunt de vectors linealment independents que generen l’espai vectorial mitjançant combinacions lineals, és a dir, tals que qualsevol vector v de l’espai pot ésser expressat d’una manera unívoca com a combinació lineal dels vectors de la base:
Les coordenades a 1 ,, a n de v en la base e 1 ,, e n són úniques Tot espai vectorial té una base és una conseqüència de l’axioma de Zermelo Si l’espai E té una base formada per un nombre finit d’elements base finita l’espai és de dimensió finita aleshores totes les bases tenen el mateix nombre d’elements, nombre que s’anomena la dimensió de l’espai , dim E Un espai vectorial de dimensió finita té infinites bases Dues bases de E , B = e 1 ,, e n i B’ = e’ 1 ,, e’ n es relacionen mitjançant una matriu de canvi de base essent és a dir, les matrius A i B són inverses B = A…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina