Codi o xifratge de Hill
-
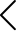
- Home
-
- 7 of 32
En l’article d’avui, us parlaré de la codificació amb matrius usant aritmètica modular, a partir de l’exemple del codi o xifratge de Hill.
Qualsevol text el podem escriure en forma de nombres, i per fer-ho, només ens cal fer correspondre a cada caràcter un número. Formalment, si tenim un alfabet de n caràcters, podem treballar en el que denotem com a (on n vol dir valors numèrics).
Per tal de xifrar un missatge, ens cal que l’emissor i el receptor es posin d’acord amb una matriu A i un vector b i fer el que indiquem a continuació.
Si anomenen x a una seqüència de nombres (per exemple, disposats com a vector columna) associats a una seqüència d’elements de l’alfabet, només cal fer:
f(x) = A · x + b = y
En aquest cas el hacker veurà que per la xarxa circula y; per esbrinar x, li caldrà saber la matriu A (de fet, la inversa de A: ).
En aquest cas,
i, per tant,
.
Tanmateix, per poder fer totes aquestes conversions cal que existeixi la matriu inversa en , condició que es compleix si
mcd (det(A), n) = 1.
I per això, n’hi ha prou escollint n primer.
El primer model de xifratge senzill el trobem en l’anomenat codi o xifratge de Hill.
 El matemàtic nord-americà Lester S. Hill (1891-1961), l'any 1929, va realitzar una aportació fonamentada en combinar l'àlgebra lineal i l'aritmètica modular. Hill va publicar l'article "Cryptography in an Algebraic Alphabet", a la revista American Mathematical Monthly (vol. 36, núm. 6, juny-juliol, 1929, p. 306-312), en el qual descriu com un bloc de text clar és xifrat a través d'una operació amb matrius. Demostra que és possible utilitzar una matriu, en principi d'ordre dos, com a eina per xifrar un missatge en paraules, descomponent el text en parells de lletres i associant a cada lletra de l'alfabet un valor numèric.
El matemàtic nord-americà Lester S. Hill (1891-1961), l'any 1929, va realitzar una aportació fonamentada en combinar l'àlgebra lineal i l'aritmètica modular. Hill va publicar l'article "Cryptography in an Algebraic Alphabet", a la revista American Mathematical Monthly (vol. 36, núm. 6, juny-juliol, 1929, p. 306-312), en el qual descriu com un bloc de text clar és xifrat a través d'una operació amb matrius. Demostra que és possible utilitzar una matriu, en principi d'ordre dos, com a eina per xifrar un missatge en paraules, descomponent el text en parells de lletres i associant a cada lletra de l'alfabet un valor numèric.
La matriu per xifrar el text pla l’anomenem A (serà la clau), invertible, que per senzillesa la considerem determinant de la unitat, i d’aquesta manera garantim que sigui invertible i que
mcd (det(A), n) = 1.
Notem que tindrem possibles parelles, fet que en dificulta la vulnerabilitat. El xifratge de Hill es pot generalitzar per blocs formats per k caràcters (amb k > 2) amb matrius d’ordre k; amb això tindrem
possibilitats.
En resum, si anomenem A la matriu clau, tindrem
amb
det(A) = ad-bc = 1, (o mcd(det (A), n) = 1),
amb
.
Així, per xifrar:
en mòdul n, on el missatge és
.
Mentre que per desxifrar, apliquem la matriu inversa a .
Per il·lustrar el funcionament del xifratge de Hill ho farem amb l’alfabet català (posem la ç al lloc on aniria la ñ de l’alfabet espanyol) ampliat amb l'espai blanc que designarem amb el símbol @, i on cada caràcter s'identifica amb un nombre —per senzillesa, en l'exemple, es pren el nombre d'ordre.
Treballarem a i l’alfabet considerat és el que mostrem:
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
Ç |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
@ |
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
D’aquesta manera, cada missatge a xifrar es descompon en blocs de dos elements.
Posem un exemple. Xifrem la paraula MAT.
Per fer-ho, agrupem MAT en blocs de dos elements de la forma MA T@. A cada caràcter se li associa el nombre d’ordre corresponent, en el nostre cas MA s'identificarà amb (12 0) i T@ amb (20 27).
Ara, aplicarem la clau , coneguda per l’emissor i el receptor:
MA quedarà en mòdul 28 com .
T@ quedarà en mòdul 28 com .
Per tant, la paraula MAT xifrada alfabèticament és IACW, i en aquest cas al hacker li caldria desxifrar el missatge IACW.
En síntesi, les operacions matricials efectuades tenen com a model matemàtic el producte de matrius de la forma:
=
.
Per desxifrar, es considera la matriu inversa:
També es pot compactar amb un sol producte de matrius com:
,
on podem multiplicar per la inversa i s’obté:
=
=
.
En aquesta tipologia de codificació també s'hauria pogut considerar l’ordenació de l’alfabet en una transformació afí, de manera que a la lletra que ocupa el lloc k li fem correspondre el lloc en mòdul n per a certs a i b, nombres naturals escollits convenientment amb mcd(a,n) = 1 per garantir que a tingui invers. El codi de Cèsar seria un cas particular amb a = 1 i en general b = 3.