Resultats de la cerca
Es mostren 125 resultats
figures de Penrose
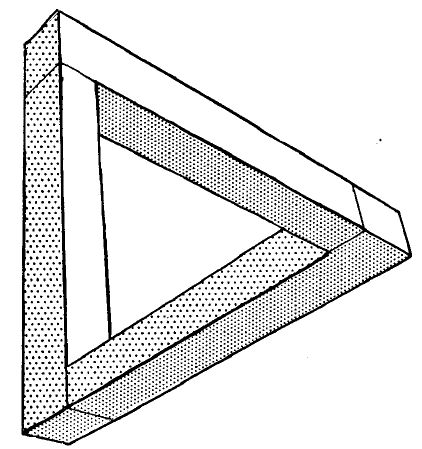
Triangle de Penrose
Representacions bidimensionals de figures tridimensionals que no poden existir en un espai euclidià ordinari.
El físic i matemàtic Roger Penrose féu popular la representació d’un triangle format per tres trams rectes de secció quadrada units formant un angle recte en cadascun dels extrems
políedre
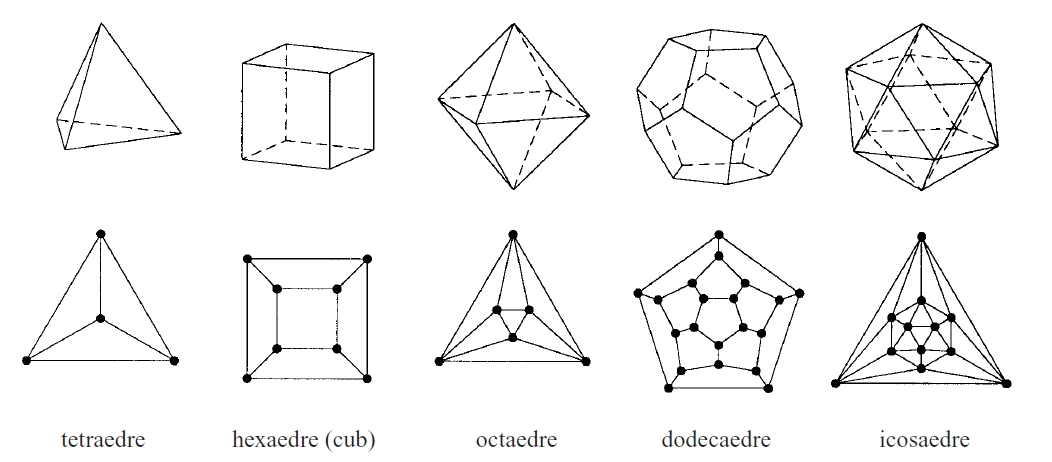
Els cinc políedres regulars i els diagrames de Schlegel associats
© Fototeca.cat
Matemàtiques
Sòlid limitat per quatre o més polígons anomenats cares.
Les interseccions de les cares constitueixen les arestes , i les interseccions de les arestes, els vèrtexs Un políedre és convex si qualsevol secció plana del políedre és un polígon convex Un políedre és còncau si no és convex Un políedre és simple si és topològicament equivalent a una esfera, és a dir, si no té forats Un políedre és regular si té les cares iguals i els angles iguals, essent les cares polígons regulars Des de la Grècia antiga hom sap que existeixen solament cinc políedres regulars el tetràedre regular , l’…
semblant
Matemàtiques
Dit dels polígons que, tenint angles iguals, tenen costats proporcionals.
Zenodor
Matemàtiques
Matemàtic grec de l’escola d’Alexandria.
Comparà les superfícies dels polígons isoperímetres i arribà a la conclusió que el cercle és el que enclou l’àrea màxima arribà també a una conclusió anàloga pel que fa a l’esfera
escalenòedre
Mineralogia i petrografia
Sòlid cristal·logràfic limitat per triangles escalens, la meitat dels quals s’ajunten a cada extrem de l’eix principal de simetria, i amb arestes polars alternativament llargues i curtes.
Les arestes laterals del sòlid formen polígons esbiaixats que, vists des de dalt, ofereixen l’aspecte d’un polígon regular N’hi ha dues classes, ditrigonal i tetragonal , segons quin sigui l’eix principal de simetria
esquerda de dessecació

Esquerdes de dessecació a Pucusana, prop de Lima (Perú)
Miguel Vera León (CC BY 2.0)
Geologia
Esquerda que es produeix per dessecació de la superfície d’un dipòsit sedimentari de gra fi.
Aquestes esquerdes s’encreuen entre si i divideixen la superfície del terreny en polígons irregulars que poden mesurar des de pocs millímetres fins a un metre de diàmetre Quan es troben fossilitzades en dipòsits antics s’empren com a indicadors ambientals i de polaritat dels estrats
polítop
Matemàtiques
Conjunt de punts de l’espai ℝn limitat per hiperplans.
La noció de politop generalitza la de polígon i la de políedre De fet, els politops de ℝ 2 són els polígons i els politops de ℝ 3 són els políedres Un exemple de politop a ℝ 4 és el tesseractis , que és l' hipercub de quatre dimensions
mosaic
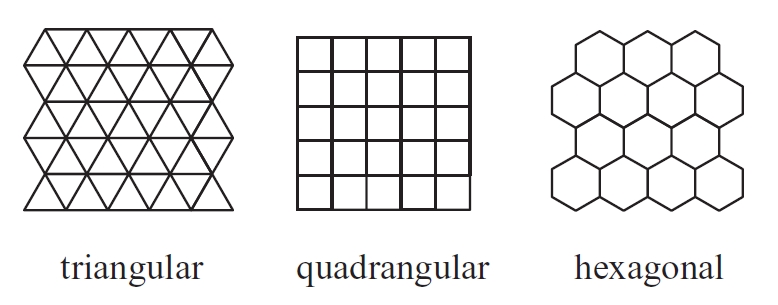
mosaics
© Fototeca.cat
Matemàtiques
Recobriment del pla per repetició d’un mòdul fix segons dues direccions.
Els mosaics regulars s’obtenen per repetició d’un polígon regular Els mosaics semiregulars es generen en combinar dos tipus de polígons regulars de dimensions convenients per al seu acoblament Únicament hi ha tres tipus de mosaics regulars i vuit de semiregulars Els únics mosaics regulars que es poden construir al pla són el triangular, el quadrangular i l’hexagonal
Bonavista
Barri
Barri del municipi de la Canonja .
Format els anys seixanta prop la carretera de Barcelona a València, sense cap pla d’urbanització, pertanyia a l’antic municipi de la Canonja, incorporat a Tarragona el 1964 Sorgí en establir-s’hi un gran nombre d’immigrants treballadors dels polígons industrials pròxims i de la construcció per al turisme a Salou, i vint anys després la població s’havia quadruplicat posteriorment, ha tendit a minvar El 2010 tornà a formar part del nou terme municipal de la Canonja
Polinèsia Francesa

L’illa de Tahaa
Adam Reeder (CC BY-NC 2.0)
Arxipèlag
Territori no independent
Territori francès d’ultramar, format per un centenar d’illes i illots: Societat, Marqueses, Australs, Tuamotu, Gambier, Clipperton, que ocupen la major part de la Polinèsia Meridional.
La capital és Papeete , a Tahití Són d’origen volcànic o corallí El clima és tropical amb variacions latitudinals Població polinèsia sobretot maoris amb nombrosos mestissos i xinesos i francesos La palmera cocotera és el principal recurs, però hi ha altres conreus cotó, canya de sucre, cafè Pesca i ramaderia en algunes illes Produeixen copra, sucre, rom i objectes de nacre Exporten copra, vainilla Societat, nacre Tuamotu i Societat El Centre d’Expérimentation du Pacifique CEP, per a les experiències nuclears franceses, té polígons atòmics als atols de Fangataufa i Mururoa i ha convertit el…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina