Resultats de la cerca
Es mostren 24 resultats
resultant
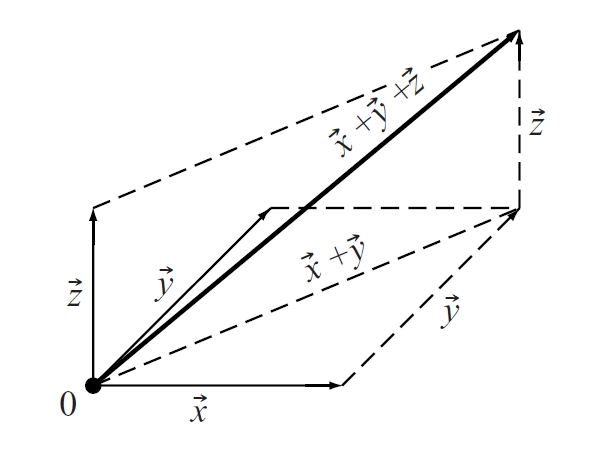
Resultant d’una suma de vectors
Física
Vector equivalent a la suma de dos vectors.
Donats dos vectors, hom n'obté la resultant per la regla del parallelogram cal construir un parallelogram que tingui per costats els vectors donats, i la resultant és aleshores la diagonal d’aquest parallelogram
bra
Física
En la notació de Dirac de la mecànica quàntica, vector dual d’un ket
, introduït per a realitzar productes escalars de vectors.
S'aplica com a funcional lineal continu sobre els kets = , essent aquest darrer el producte escalar dels dos vectors |ψ> i |Φ>
llei de les àrees
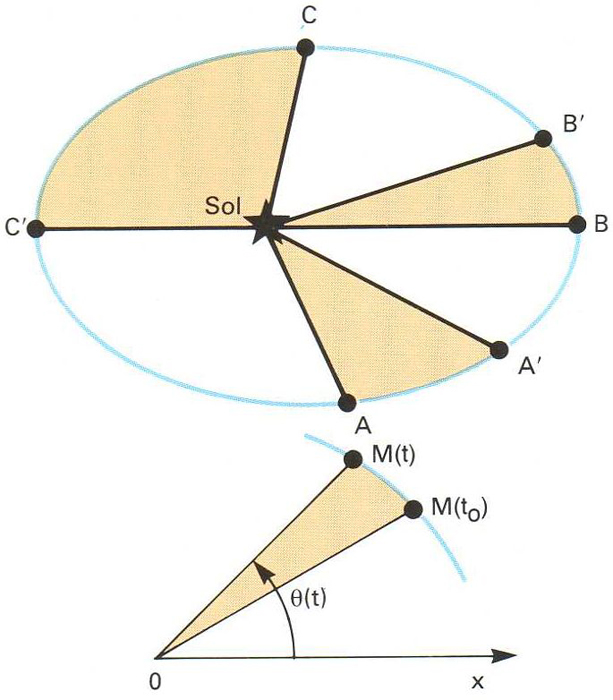
Llei de les àrees aplicada a l’òrbita d’un planeta: les àrees contingudes entre els punts AA’, BB’ i CC’ són iguals perquè es recorren en temps iguals. El radi vector escombra àrees iguals en temps iguals
© fototeca.cat
Física
Teorema referit al moviment d’un punt sotmès a un sistema de forces centrals, que demostra que les àrees descrites pels radis vectors r
©són proporcionals al temps emprat per a descriure-les.
En astronomia, aquest teorema és aplicat a l’estudi del moviment d’un planeta respecte al Sol i és conegut com la segona de les tres lleis de Kepler La demostració és obtinguda d’aplicar el teorema del moment angular al cas particular del moviment d’un punt material M sotmès a un sistema de forces centrals que passen pel punt O , respecte al qual hom obté els moments Aquests moments tenen una resultant nulla i, per tant, el moment angular L és un vector constant perpendicular sempre als radis vectors, que descriuran com a conseqüència una trajectòria plana Si hom considera la posició de M en…
vector
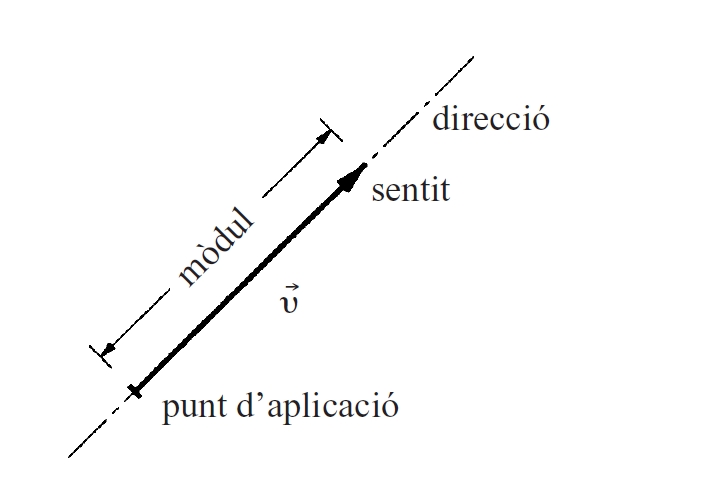
Vector
Física
Matemàtiques
Element d’un espai vectorial.
Des del punt de vista geomètric, a tot vector se li pot associar direcció, mòdul i sentit, i un punt d’aplicació Segons les seves posicions relatives, es parla de vectors simètrics, oposats, conjugats, ortogonals, etc Fixada una base de vectors e 1 ,, e n en un espai vectorial E de dimensió n base d’un espai vectorial, tot vector x de E pot ésser expressat en forma única com a combinació lineal dels elements de la base x = x 1 e 1 + + x n e n Així, x resta determinat pels nombres x 1 , x 2 ,, x n , els quals són dits components de x hom ho escriu x = x 1 ,, x n…
moment d’un vector respecte a una recta
Física
Donats un vector i una recta, component segons la recta del moment del vector respecte a un punt qualsevol de la recta.
Pot ésser demostrat que aquesta component no depèn del punt de la recta escollit En el cas que el vector representi una força, hom parla del moment de la força respecte a la recta Si, en comptes d’un únic vector, hi ha un sistema de vectors, hom anomena moment resultant del sistema de vectors respecte a la recta la suma dels moments de cadascun dels vectors respecte a la recta
moment d’un vector respecte a un punt
Física
Donat un punt A i un vector v aplicat en un punt P, vector M igual al producte vectorial del vector AP pel vector v, és a dir, M = AP ∧ v
.
En el cas que el vector v representi una força, el vector M és anomenat moment de la força respecte al punt A Si en comptes d’un únic vector v hi ha un sistema de vectors, hom anomena moment resultant del sistema de vectors respecte al punt A la suma dels moments de cadascun dels vectors respecte al punt A En el cas particular que el sistema de forces sigui un parell de forces , el moment resultant és anomenat moment del parell El moment d’un parell té la propietat d’ésser el mateix, qualsevol que sigui el punt donat A
degeneració
Física
En mecànica quàntica, propietat d’un valor propi d’un observable, segons la qual hi ha diferents estats propis de l’observable que tenen per valor propi el considerat.
La dimensió del subespai de vectors propis amb valor propi a és la multiplicitat o degeneració de a
polígon de forces
Física
Construcció gràfica que serveix per a trobar la resultant d’un sistema de forces qualsevol.
Si F 1 , F 2 , F 3 són les forces, la resultant R és obtinguda dibuixant vectors fixos representants de F 1 , F 2 , F 3 , de manera que l’extrem de cadascun sigui l’origen del següent R és el vector lliure representat pel vector fix que comença a l’origen de F 1 i acaba a l’extrem de F 3
hamiltonià
Física
Operador sobre l’espai de Hilbert d’un sistema físic descrit per la mecànica quàntica, que representa l’energia observable.
Pot ésser obtingut del hamiltonià del corresponent sistema clàssic substituint coordenades i moments pels corresponents operadors Els seus valors propis són els valors possibles de l’energia espectre d’energies i els vectors propis són els estats estacionaris Incorpora la dinàmica concreta del sistema en l’equació de Schrödinger , on |ψ t > és un estat del sistema ket i h és la constant reduïda de Planck
llei de Biot i Savart
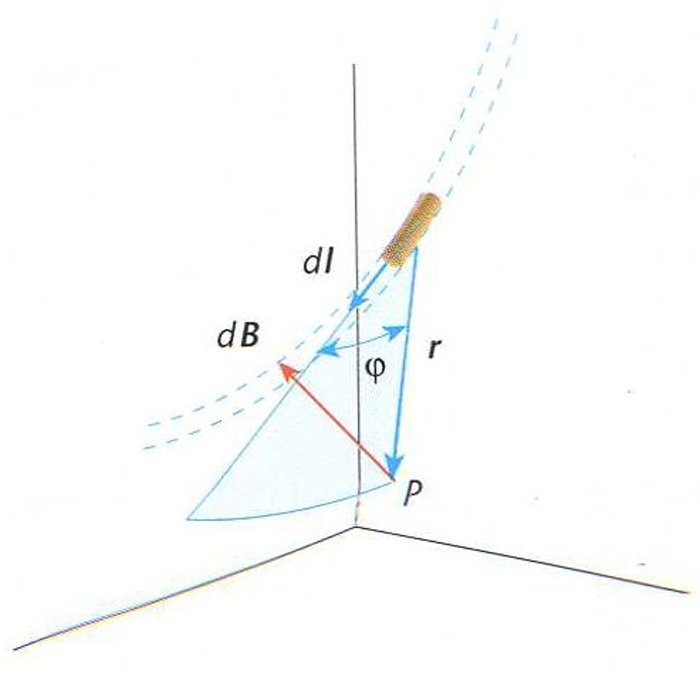
Llei de Biot i Savart
© Fototeca.cat
Electrònica i informàtica
Física
Llei que dóna la inducció magnètica dB en un punt qualsevol P de l’espai, produïda per un element de corrent Idl que circula per un conductor:
essent μ 0 la permeabilitat magnètica del buit, I la intensitat del corrent, r la distància de l’element de corrent a P i θ l’angle entre els vectors d l i r En forma vectorial s’expressa per El camp total, suma de les contribucions de tots els elements de corrent es calcula fent Si el conductor és rectilini, aquesta expressió dóna el resultat essent R la distància perpendicular entre el conductor i el punt P en qüestió Quan les condicions de simetria ho permeten el camp magnètic pot calcular-se mitjançant el teorema d’Ampère