Resultats de la cerca
Es mostren 3270 resultats
resoldre un triangle
Matemàtiques
Determinar, a partir dels elements coneguts, els altres elements desconeguts (costats i angles) d’un triangle donat.
resoldre
Matemàtiques
Trobar la solució d’una equació o d’un sistema d’equacions o inequacions.
punt de retrocés
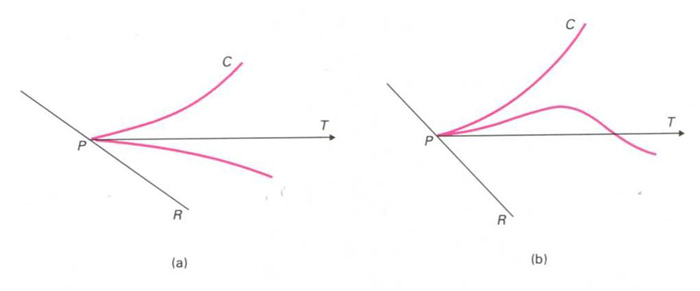
Punt de retrocés de primera (a) i de segona (b) espècie
© fototeca.cat
Matemàtiques
Donada una corba plana C
, punt P
d’aquesta corba en el qual existeix una tangent T
de tal manera que existeix un entorn U
de P
i una recta R
, diferent de T
, tals que els punts de C ∩U
pertanyen al mateix semiplà respecte a R
.
És un punt de retrocés de primera espècie si existeix un entorn U´ de P tal que els punts de C ∩U´ són repartits entre els dos costats de T , i és un punt de retrocés de segona espècie si són al mateix costat respecte a T Un punt de retrocés és anomenat també cúspide o punt cuspidal
retracte
Matemàtiques
Conjunt tancat que és imatge per una aplicació contínua d’un conjunt més ampli que el conté en un espai topològic.
Així, per exemple, un cercle és el retracte del quadrat circumscrit que el conté
reticle
Matemàtiques
Conjunt ordenat en el qual dos elements qualssevol tenen un suprem (la més petita de les fites superiors o elements majorants) i un ínfim (la més gran de les fites inferiors o elements minorants).
És anomenat també conjunt reticular Si C, ≤ és un “ordenat” que és reticle, donats a i b de C, existeix un element, anomenat suprem c = a ∪ b tal, que a ≤ c , b ≤ c , i si a < d i b < d és c < d i un element, dit ínfim , c = a ∩ b tal, que c < a, c < b i si d ≤a, d ≤ b , és d ≤ c El conjunt de parts d’un conjunt respecte a l’ordre definit per la inclusió és un reticle Exemple si A i B són dos conjunts qualssevol, el conjunt més petit que els conté és la seva reunió o suprem i el més gran contingut és la seva intersecció o ínfim La teoria de reticles nasqué amb l’estudi del…
taxonomia
Matemàtiques
Branca de les matemàtiques que estudia problemes de classificacions.
La teoria matemàtica de la taxonomia versa, doncs, sobre el tractament rigorós de les eines matemàtiques que comporta l’estudi de les classificacions, des de les estructures abstractes generadores de classificacions de diferents tipus com particions amb encavalcament preordres, particions equivalències, arbres ordres estratificats, jerarquies, similituds, etc, fins a mesures del “poder separador” de les classificacions índexs de distància i de similitud, estructures ultramètriques Tracta tant sobre els criteris com sobre els algorismes per a la descripció matemàtica de les classificacions El…
concoide d’una corba respecte a un punt
Matemàtiques
Donada una corba C
i un punt O
del seu pla, lloc geomètric dels punts Q
i Q’
determinats en mesurar, a ambdós costats, una determinada distància b
a partir del punt P
obtingut en tallar la corba C
mitjançant una recta R
que passi per O
.
De la definició resulta palès que la concoide d’una corba té dues branques Si C és una recta, i hom escull un sistema de coordenades polars amb origen al punt O , separat de C per una distància perpendicular a , l’expressió de la concoide de la recta C respecte a O és r= a/cos θ+ b si a < b es determina un llaç en O , si a = b hi ha una cúspide en O i la concoide és la concoide de Nicomedes , i si a > b no hi ha cúspide però hi ha un acnode en O Un altre cas particular s’escau quan C és una circumferència en aquest cas, la concoide de la circumferència C respecte a un dels seus punts…
concoide
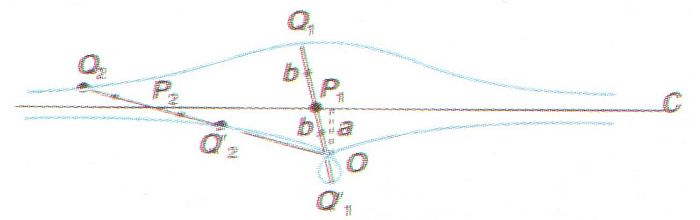
Concoide d’una recta C respecte a un punt O, en el cas de formació d’un llaç en O(a major que b); es satisfà que P2Q2 = P2Q2' = b = P1Q1 = P1Q1'
©
Matemàtiques
Corba plana d’equació x2 y2=(a+y2 ) (b2- y2 ), on a i b són dues constants.
component
Matemàtiques
Dit de cadascun dels factors que componen un vector
o un tensor tensor de Riemann [tensor]
.
complement d’una part d’un conjunt
Matemàtiques
Donada una part A
d’un conjunt C, A ⊂C,
subconjunt de C
format pels elements de C
que no pertanyen a A
; és representat per CA
.
De manera menys precisa, hom pot definir també el complement d’un conjunt qualsevol C , com el complement del conjunt respecte al conjunt universal format per tots els possibles elements de tots els possibles conjunts, és a dir, el complement de C és el conjunt C' tal que C ∪ C' = U i C ∩ C' = ∅on U és el conjunt universal