Resultats de la cerca
Es mostren 1486 resultats
el·lipse
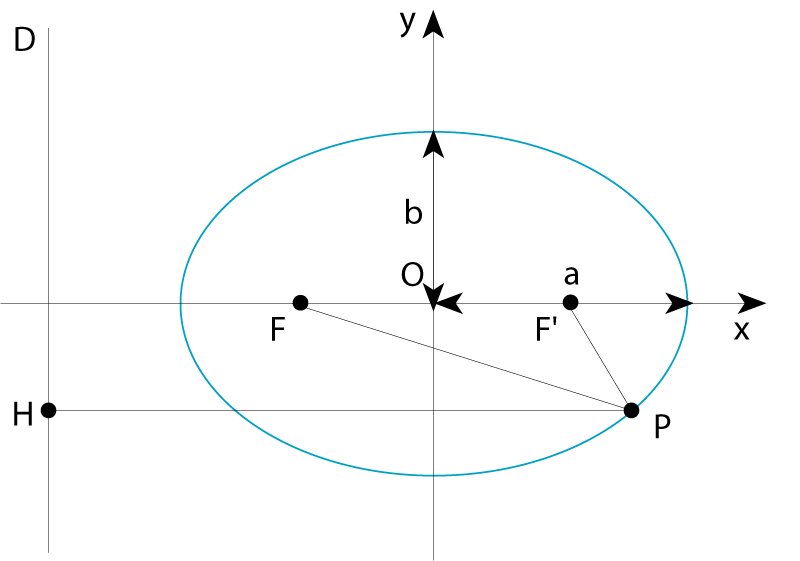
El·lipse de semieixos a i b; D és la directriu associada al focus F
© Fototeca.cat
Matemàtiques
Corba tancada que resulta de la intersecció d’una superfície cònica amb un pla que no és paral·lel a cap generatriu ni a l’eix d’aquella; és doncs, una cònica
.
La seva equació en coordenades cartesianes referides als seus dos eixos perpendiculars de simetria és x 2 / a 2 + y 2 / b 2 =1, a essent el semieix major i b el semieix menor L’ellipse és el lloc geomètric dels punts P del pla tals que la suma de llurs distàncies a dos punts fixos F i F ´, anomenats focus , és una quantitat constant, independent del punt P concret, igual al doble del semieix major, PF + PF ´=2 a és també el lloc geomètric dels punts P tals que el quocient de llurs distàncies a un punt fix, un dels focus, i a una recta…
evoluta
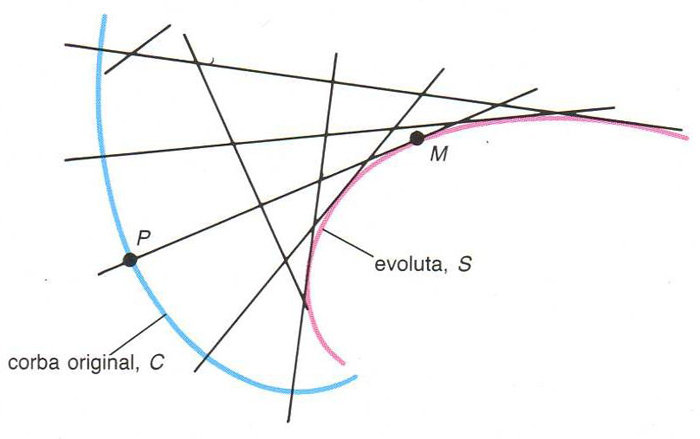
La corba S és l’evoluta de C
© fototeca.cat
Matemàtiques
Donada una corba plana C
, lloc geomètric dels centres de curvatura de C
.
És l'envolupant S de les normals a la corba C així, una normal en el punt P a C és tangent a l’evoluta i el punt de tangència M és el centre de curvatura de C en el punt P Si S és l’evoluta de C , C és una evolvent de S L’evoluta d’un cercle es redueix a un punt
raó doble
Matemàtiques
Donats quatre punts alineats A, B, C i D, relació
.
La raó doble és un invariant en una projecció
equador
Matemàtiques
Cercle que talla perpendicularment, per la meitat, els meridians d’una superfície de revolució, és a dir, que és el màxim dels seus paral·lels.
quocient
Matemàtiques
Nombre que resulta de la divisió d’un nombre (dividend) per un altre (divisor); així, el quocient de 24 per 8 és 3.
En general, el dividend és igual al producte del quocient pel divisor, més el residu o resta
decimal
Matemàtiques
Dit de la fracció el denominador de la qual és una potència de deu.
esfera
Matemàtiques
En un espai mètric de distància d, conjunt de punts x la distància dels quals a un cert punt fix p és igual a un nombre real positiu r.
El centre de l’esfera és p i el radi r , i es denota per S p r A ℝ n l’esfera de centre 0 i radi 1 es denota per S n –1 i rep el nom d’ esfera unitat