Resultats de la cerca
Es mostren 56 resultats
entorn
Matemàtiques
En un espai topològic E, part de E que conté un obert de E que al seu torn conté un punt x o una part A de E; en el primer cas, hom parla d’entorn d’un punt, i, en el segon, d’entorn d’una part de E
.
entorn
Matemàtiques
A l’interior d’una figura geomètrica fitada, conjunt de punts que disten d’un punt donat en menys d’una certa quantitat.
sòlid de revolució
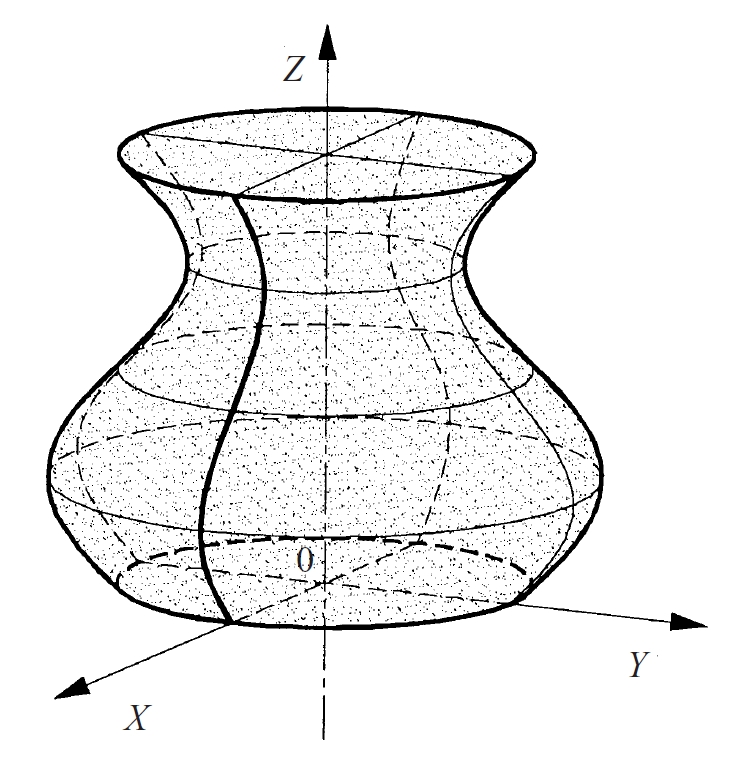
sòlid de revolució
Matemàtiques
Cos limitat per una superfície de revolució, que hom obté per la rotació d’una línia entorn d’un eix.
Així, l’esfera és el sòlid engendrat per un cercle que gira entorn d’un diàmetre el con de revolució és engendrat per una recta o un segment que talla l’eix al voltant del qual gira
residu d’una funció complexa f (z) analítica en un punt singular A aïllat
Matemàtiques
Quantitat R(f,A) = (1/2πi) ∫cf(z)dz, on C és una corba simple rectificable que envolta A en un entorn de A.
El valor del residu és igual a a-1 , on a-1 és el coeficient del terme 1/ z-A en el desenvolupament infinit de Laurent de f z en un entorn de A
punt de retrocés
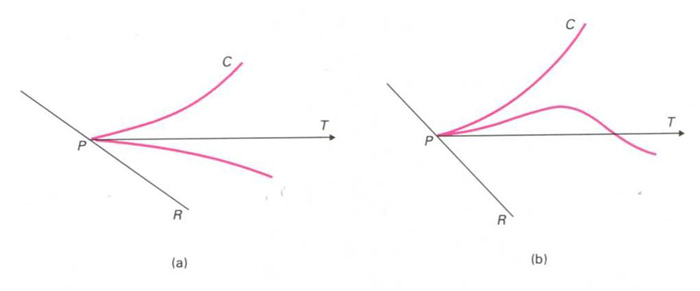
Punt de retrocés de primera (a) i de segona (b) espècie
© fototeca.cat
Matemàtiques
Donada una corba plana C
, punt P
d’aquesta corba en el qual existeix una tangent T
de tal manera que existeix un entorn U
de P
i una recta R
, diferent de T
, tals que els punts de C ∩U
pertanyen al mateix semiplà respecte a R
.
És un punt de retrocés de primera espècie si existeix un entorn U´ de P tal que els punts de C ∩U´ són repartits entre els dos costats de T , i és un punt de retrocés de segona espècie si són al mateix costat respecte a T Un punt de retrocés és anomenat també cúspide o punt cuspidal
espai localment connex
Matemàtiques
Espai topològic (X,OOO) quan en un punt x,y ∈ X si, i solament si, tot entorn d’x conté un entorn connex que conté x
.
punt adherent a un conjunt
Matemàtiques
Punt tot entorn del qual té intersecció no nul·la amb el conjunt.
Els punts adherents són o punts d’acumulació o bé lpunts aïllats
axiomes de separació
Matemàtiques
Axiomes topològics relatius a les possibles separacions entre punts.
En un espai topològic Y , els axiomes són Axioma T 0 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x que no conté y Axioma T 1 Per a qualsevol parell de punts x i y diferents, existeixen un entorn U de x , i un entorn V de y , tals que U no conté y i V no conté el punt x Quan aquest axioma se satisfà, l’espai es diu espai de Fréchet Axioma T 2 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x i un entorn de y sense punts en comú Quan aquest axioma se satisfà, l’espai s’anomena…
singularitat
Física
Matemàtiques
Dit d’un punt que presenta unes característiques diferents de les del seu entorn.