Resultats de la cerca
Es mostren 10 resultats
Brook Taylor

Brook Taylor
© Fototeca.cat
Matemàtiques
Matemàtic anglès.
Féu importants estudis sobre capillaritat, projectils, perspectiva, oscillacions, logaritmes, fluids, etc La seva aportació més important és la cèlebre fórmula per al desenvolupament en sèrie de funcions mitjançant unes diferències finites, que anomenà increments i que exposà a l’obra Methodus incrementorum directa et inversa 1715
teorema de Taylor
Matemàtiques
Teorema que dóna el desenvolupament en sèrie d’una funció f(x), fixat un punt a.
Si f x és una funció d’una variable real i derivable n vegades, la fórmula que expressa el teorema de Taylor és Els n +1 primers sumands d’aquesta expressió són coneguts com a polinomi de Taylor de grau n , per a f en el punt a , mentre que el terme R n+1 a x és anomenat resta Aquest terme compleix la següent condició d’aproximació És, per tant, un infinitèsim d’ordre superior a x-a n , i pot ésser expresat per qualsevol de les dues maneres següents per a algun t ∈ a,x , per a algun t ∈ a,x En el cas que f n⁺ 1 es pugui integrar en a,x , hom té l’expressió…
desenvolupament en sèrie
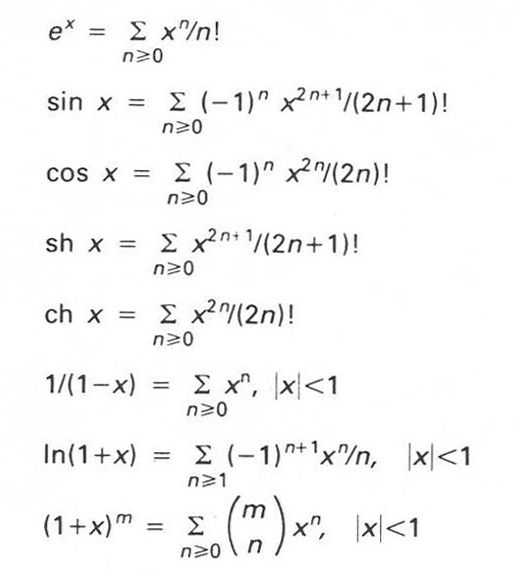
Desenvolupament en sèrie de potències d’algunes funcions
©
Matemàtiques
Expressió d’una funció real, de variable real o complexa,
f(x) ∞
, en termes d’una sèrie de funcions
:
.
La legitimitat d’aquesta igualtat depèn de la convergència de la successió de sumes parcials, en el domini de definició de fx Hom empra, generalment, el desenvolupament en sèrie de potències o sèrie entera, que resulta del teorema de Taylor , i, en el cas de funcions periòdiques, hom empra el desenvolupament en sèrie de Fourier anàlisi de Fourier
Pafnutij L’voviN Čebyšev
Matemàtiques
Matemàtic rus.
Professor de matemàtiques a la Universitat de Sant Petersburg 1853-80, fou també associé étranger de l’Institut de France i membre de la Royal Society de Londres Es destacà per les seves investigacions sobre la teoria dels nombres, el càlcul de probabilitats i alguns temes d’anàlisi teoria de les integrals, formes quadràtiques, convergència de les sèries de Taylor, etc Elaborà la teoria de les sèries de polinomis que porta el seu nom
sèrie de potències
Matemàtiques
Donada una funció real de variable real f (x) derivable indefinidament en el punt x0, sèrie Σ an (x-x0)n amb an = (1/ n !) fn (x0).
Es compleix que f x = Σ a n x- x 0 n per a tots els punts x tals que | x- x 0 | < R, on R és el radi de convergència de la sèrie Aquesta sèrie és anomenada sèrie que desenvolupa la funció f en un entorn del punt x 0 , o sèrie de Taylor de f en el punt x 0 La sèrie de potències és utilitzada per a expressar el desenvolupament en sèrie d’una funció Així, per exemple, hom té la sèrie exponencial , que és convergent per a tot x
Charles Babbage
Història
Matemàtiques
Científic i matemàtic anglès.
Ensenyà a Cambridge 1828-39 Inventà una màquina computadora basada en el mètode de les diferències, que explicà a Observations on the Application of Machinery to the Computation of Mathematical Tables 1822 Observà la manca d’institucions científiques eficaces Reflections on the Decline of Sciences in England , i això el portà a fundar la prestigiosa British Association for the Advancement of Science 1831 En On the Economy of Machinery and Manufactures 1832 analitzà les conseqüències socials de les innovacions tècniques aquest treball influí sobre els principals científics socials i també…
fórmula de Maclaurin
Matemàtiques
Fórmula que dóna el desenvolupament en sèrie de Taylor i en el punt x = 0 (teorema de Taylor) d’una funció f(x), real o complexa, derivable fins a l’ordre n + 1.
Representant per f i 0 la derivada d’ordre i de f x en el punt x = 0, la fórmula és on R, anomenat resta o terme complementari, pot ésser calculat a partir de l’expressió on θ és un nombre entre 0 i 1
regla de Simpson
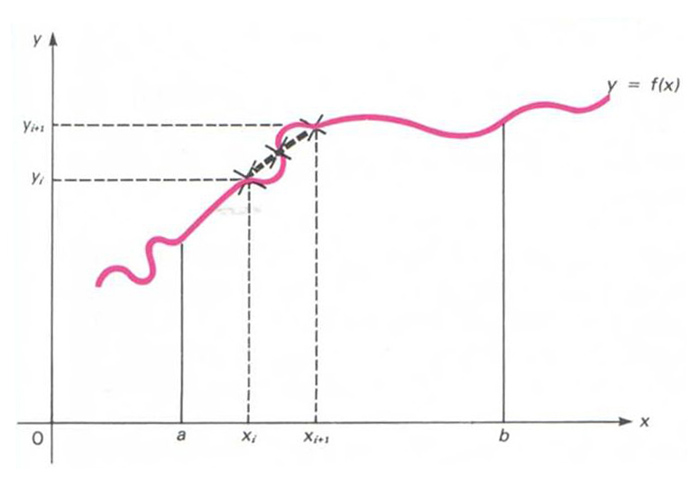
Regla de Simpson
© fototeca.cat
Matemàtiques
Mètode per a aproximar l’àrea limitada per una corba y = f(x), l’eix OX i dues rectes paral·leles x = a i x = b.
El mètode suposa que els petits arcs de la corba són aproximables mitjançant arcs de paràbola que passen pel punt mitjà i pels punts terminals de l’arc considerat La fórmula que hom obté amb aquesta aproximació és usant les sèries de Taylor fins als termes quadràtics on l’interval a,b ha estat dividit en 2 n subintervals a, x 1 , x 2 , , x 2 n - 1 , b , i y a , y 1 , y 2 , , y 2 n - 1 , y b són les respectives ordenades d’aquests punts, y i = f x i La diferència numèrica entre l’àrea real i aquesta àrea aproximativa A , és fitada per la quantitat M b-a 5 /1802 n 2 , on…
Johann Bernoulli
Matemàtiques
Matemàtic suís.
Començà estudiant medicina, però es decantà molt aviat per les matemàtiques Fou deixeble del seu germà Jakob, que l’inicià en l’obra de Leibniz, de la qual fou propagador Estigué a París 1690-95, on redactà un curs de càlcul per al marquès de L’Hôpital hom creu que la coneguda regla de L’Hôpital és deguda a Johann Bernoulli El 1691 determinà les tangents i els radis de curvatura de moltes corbes planes i donà el primer exemple de coordenades polars Fou professor a Groningen 1695-1705 i, des de la mort del seu germà Jakob, a Basilea 1705, on fou mestre d’Euler Proposà i resolgué…
anàlisi matemàtica

anàlisi matemàtica Portada dels Philosophiae Naturalis Principia Mathematica de Newton (1687)
© Fototeca.cat
Matemàtiques
Part de les matemàtiques bastida sobre els conceptes bàsics de funció, límit, continuïtat, derivada i integral.
És el desenvolupament modern del càlcul infinitesimal, elaborat durant els segles XVII i XVIII, que tenia com a principals problemes el de les quadratures determinació de la longitud d’una corba i de les àrees i volums de figures i el de la tangència traçat de tangents a corbes i superfícies Els coneixements que s’anaren acumulant sobre aquests temes formaren els càlculs integral i diferencial, cor d’aquesta disciplina matemàtica L’anàlisi matemàtica presenta els trets distintius de l’abstracció i generalitat dels seus mètodes, característics del rigor del raonament lògic És el resultat d’una…