Resultats de la cerca
Es mostren 12 resultats
teorema d’Apol·loni
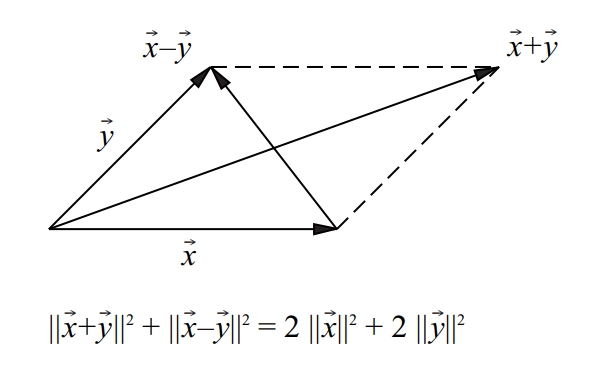
Formulació vectorial del teorema d’Apol·loni
Matemàtiques
Teorema de geomètria mètrica segons el qual en tot triangle la suma dels quadrats de dos costats és igual al doble de la suma del quadrat de la meitat del tercer costat més el quadrat de la mitjana corresponent a aquest darrer costat.
En la seva formulació actual, amb vectors i normes, aquest teorema s’anomena també llei del parallelogram i estableix que la suma dels quadrats de les dues diagonals del parallelogram és igual a la suma dels quadrats dels quatre costats
problema d’Apol·loni
Matemàtiques
Problema clàssic que proposa la construcció de les circumferències tangents a tres circumferències donades. El nombre màxim possible és 8.
cercle d’Apol·loni
Matemàtiques
Lloc geomètric dels punts del pla tals que la raó de les distàncies a dos punts fixos és constant.
Apol·loni de Perge
Matemàtiques
Matemàtic grec, darrer dels grans geòmetres hel·lènics.
De jove anà a Alexandria, on visqué i estudià al Museu viatjà, i a Pèrgam trobà l’historiador Eudem És famós el seu tractat sobre les Còniques en vuit llibres, set dels quals han estat conservats, tres a través de traduccions àrabs el vuitè fou restablert per Edmond Halley el 1646 Féu l’estudi de l’ellipse, la hipèrbola i la paràbola, corbes que poden ésser obtingudes tallant un con segons diferents plans Escriví també altres llibres on tracta diferents problemes de geometria plana, com el de la resolució del cercle que satisfà tres condicions, o els moviments en el pla Treballà en…
Robert Simson
Matemàtiques
Matemàtic escocès.
Estudià les obres dels grecs i publicà diversos tractats basats en aquestes Traduí els Elements d’Euclides 1756 i escriví Selectionum conicarum 1735, seguint l’estil d’Apolloni
Isaac Barrow
Matemàtiques
Cristianisme
Matemàtic i teòleg anglès.
Professor a Cambridge, cedí el lloc al seu deixeble Newton Fundà la biblioteca del Trinity College Fruit dels seus cursos són les Lectiones opticae 1669 i les Lectiones geometricae 1670 Féu importants aportacions al naixent càlcul infinitesimal i a la geometria, i edità Euclides, Arquimedes i Apolloni L’obra Treatise on the Pope's Supremacy 1680 és de caràcter polèmic
Aristeu de Crotona
Matemàtiques
Matemàtic grec.
Escriví cinc llibres sobre Els llocs sòlids on formulà teoremes sobre els cinc sòlids regulars i sobre les corbes còniques Influí sobre Euclides, bé que el tractat d’Aristeu és més important i original Les seves obres només són conegudes per referències de Pappus i Euclides Això fa que tota l’originalitat de l’estudi de les còniques recaigui sobre Apolloni de Perge
Hipàcia
Matemàtiques
Matemàtica, metgessa i filòsofa.
Escrigué un comentari als sis primers llibres de l' Aritmètica de Diofant i també un tractat sobre les Còniques d' Apolloni El seu pare fou Teó d'Alexandria , prestigiós matemàtic i astrònom, del qual aprengué els descobriments astronòmics de Ptolemeu Es preocupà d’editar l' Almagest , l’obra més important d’aquest insigne astrònom grec Fou una defensora indiscutible de la filosofia neoplatònica i s’oposà a la implantació del cristianisme al Museu d’Alexandria, del qual fou el darrer director Morí assassinada al carrer en mans de cristians fanàtics en veure que no volia convertir-se a la fe…
cònica
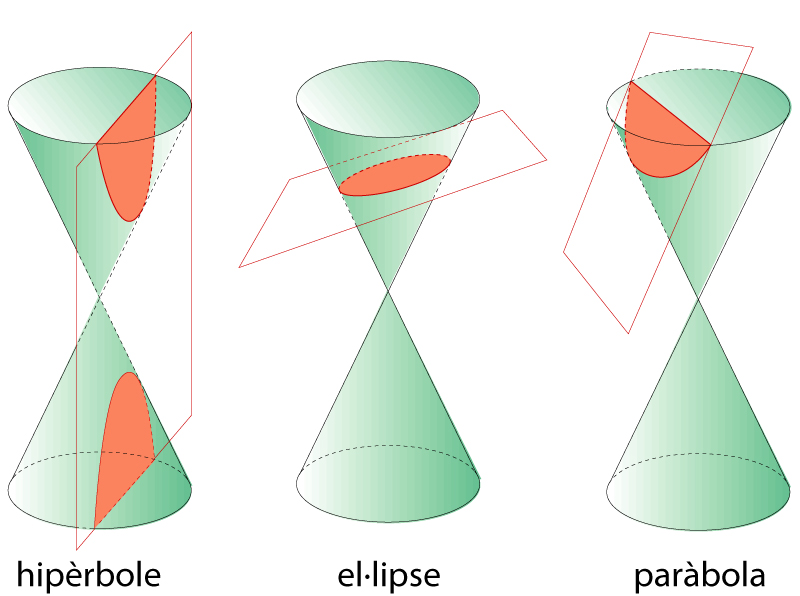
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la…
geometria
Matemàtiques
Part de la matemàtica basada en la intuïció d’espai.
El nom prové de la seva primera aplicació la mesura de la Terra Els diversos apartats en què hom divideix la geometria fan referència a la natura dels objectes d’estudi i al mètode emprat Per a una definició unitària de la geometria elemental, l’any 1872 CF Klein proposà,en el “programa d’Erlangen”,la noció de geometria com a consideració d’un espai el conjunt dels punts i un grup de transformacions d’aquest espai, els invariants del qual serien les nocions de la geometria en qüestió El primer estudi de la geometria fou de caràcter intuïtiu, i consistí en la compilació de fets relatius a…