Resultats de la cerca
Es mostren 21 resultats
gnòmon
gnòmon
© Fototeca.cat
Matemàtiques
Figura geomètrica que, unida amb una altra, fa una figura semblant a aquella.
gradient
Física
Matemàtiques
Donada una funció f
derivable i definida en una regió de l’espai ℝ 3
, funció vectorial (grad f
o ∇ f
) definida per la fórmula
.
En cada punt, és un vector perpendicular a la superfície f = constant, que passa pel punt en què és calculat, i, per tant, té la direcció en la qual varia més ràpidament Per extensió, hom anomena gradient d’una funció en una direcció o derivada direccional la projecció del vector gradient en aquella direcció Així, fixada una direcció, el gradient d’una funció en aquella direcció dóna el ritme de variació de la funció en avançar en la direcció considerada En meteorologia i en física de fluids són molt utilitzats els gradients tèrmics i baromètrics per a referir-se a les variacions de…
equació funcional
Matemàtiques
Relació imposada a una funció.
Una tal relació defineix una funció o família de funcions que satisfan aquella relació
Ernest William Brown
Astronomia
Matemàtiques
Astrònom i matemàtic anglès.
Professor de matemàtiques aplicades al Haverford College Pennsilvània 1891-1907 i a la Universitat de Yale 1907-32, investigà dins el camp de la mecànica celeste Les seves taules de la Lluna 1920 resten com el millor treball sobre el complex moviment d’aquella Exposà l’existència d’irregularitats en el moviment de rotació de la Terra 1926 i investigà sobre les teories planetàries, els asteroides i la ressonància
Sebastià Dionís Colera d’Avinent
Esoterisme
Matemàtiques
Matemàtic i astròleg.
Professà al convent del Carme de València Disputà amb Tosca sobre qüestions matemàtiques No havent aconseguit la càtedra de matemàtiques de la Universitat de València, anà a Salamanca, on obtingué la d’aquella universitat Publicà un Juicio nuevo sobre los varios cometas que se han admirado sobre el horizonte de Valencia 1681 i Suma astronomológica , síntesi dels escrits d’astronomia i d’astrologia més coneguts de la seva època
rotacional
Física
Matemàtiques
Operador diferencial definit sobre un camp vectorial A
per la fórmula:
on ∇ és l’operador gradient
.
El teorema de Stokes permet d’interpretar intuïtivament l’operador rotacional quan rot A = 0 en una zona de l’espai, la circulació del camp vectorial A al llarg d’una línia tancada situada en aquella zona sol ésser diferent de 0 En particular, per al camp gravitacional g resulta rot g = 0, i per als camps elèctric i magnètic és rot E = -∂ B /∂ t i rot B = μ o j + μ o ε o
oblic | obliqua
Matemàtiques
Dit del prisma determinat per la intersecció d’una superfície prismàtica amb dos plans no perpendiculars a les arestes d’aquella.
Johann Franz Encke
Astronomia
Matemàtiques
Astrònom i matemàtic alemany.
Deixeble de Gauss, l’any 1816 fou nomenat astrònom de l’observatori de Gotha Més tard esdevingué director de l’observatori de Berlín i professor de la Universitat d’aquella mateixa ciutat Els seus treballs més importants es relacionen amb l’estudi dels cometes Calculà els elements de l’òrbita d’una sèrie de cometes observats entre el 1680 i el 1818 i demostrà que corresponien a un mateix cos celeste, que després batejà amb el propi nom També calculà la parallaxi solar a partir de les dades obtingudes gràcies als passos de Venus davant el Sol, que s’esdevingueren els anys 1761 i 1769
mètode dels mínims quadrats
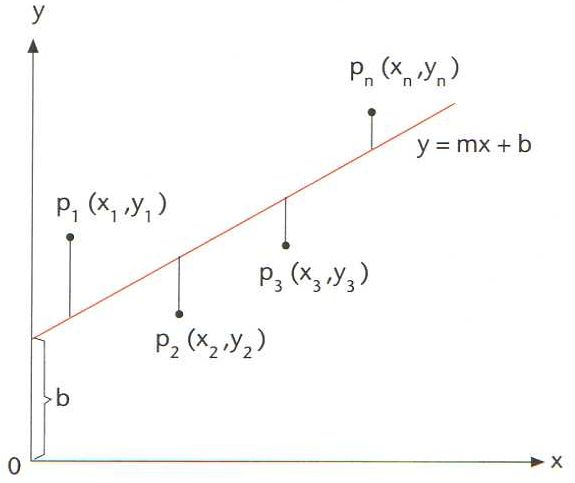
Representació de la recta y=mx + b obtinguda pel mètode dels mínims quadrats
© Fototeca.cat
Matemàtiques
Donat un conjunt de n punts del pla (x1, y1), (x2, y2), ... (xn, yn), mètode que permet de trobar l’equació y = mx + b de la recta que compleix la condició d’ésser la que més s’apropa als punts donats.
Hom defineix matemàticament la dita condició exigint que la suma dels quadrats de les desviacions, ha d’ésser mínima, entenent per desviació en un punt x i , y i la diferència d i = y i - mx i + b Hom pot demostrar que aquella condició condueix a les dues equacions a partir de les quals hom pot calcular els coeficients m i b de la recta, la qual és anomenada també recta de regressió D’altra banda, el mètode dels mínims quadrats serveix també per a ajustar funcions més complexes que la d’una recta, tals com funcions polinòmiques, exponencials, etc, i és utilitzat en l’estudi…
asímptota
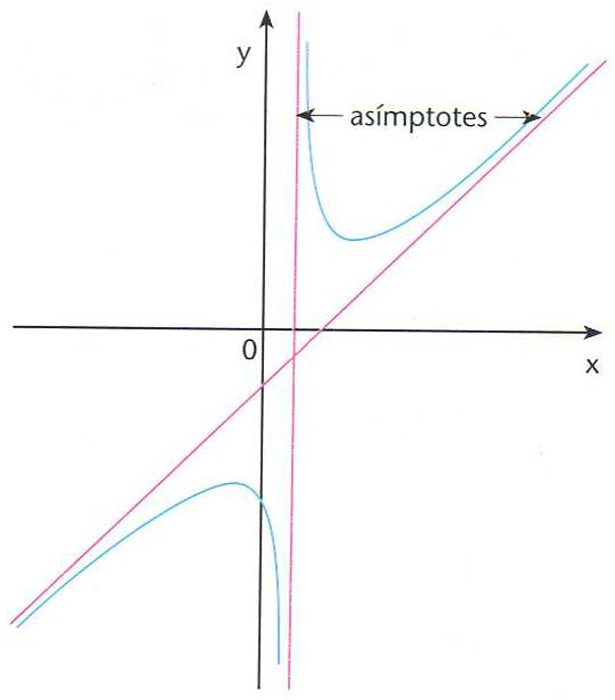
Asímptotes
Matemàtiques
Recta a la qual s’acosta un punt variable sobre una branca de corba quan el punt s’allunya cap a l’infinit.
Per a poder afirmar que una branca de corba té una asímptota cal que, si el punt P es mou sobre aquesta de manera que la distància de P a l’origen de coordenades O creix infinitament, la direcció de la recta OP tingui un límit determinat Hom troba aquest límit per mitjà del quocient y/x = tg a Coneguda la direcció de l’asímptota, hom determina la seva ordenada a l’origen per la condició que la distància entre dos punts que tinguin igual abscissa, un sobre la corba, l’altre sobre l’asímptota, tingui límit zero quan aquella abscissa comuna es fa infinita Així, per exemple, la…