Resultats de la cerca
Es mostren 139 resultats
C
Matemàtiques
Cpq designa el nombre de combinacions d’ordre q, formades a partir de p elements.
constant d’Euler
Matemàtiques
Límit quan n →∞; de la sèrie {un}, n>0, de terme general un= 1+1/2+1/3+...+ 1/n-ln n.
El seu valor aproximat és C = 0,577 215 66
evoluta
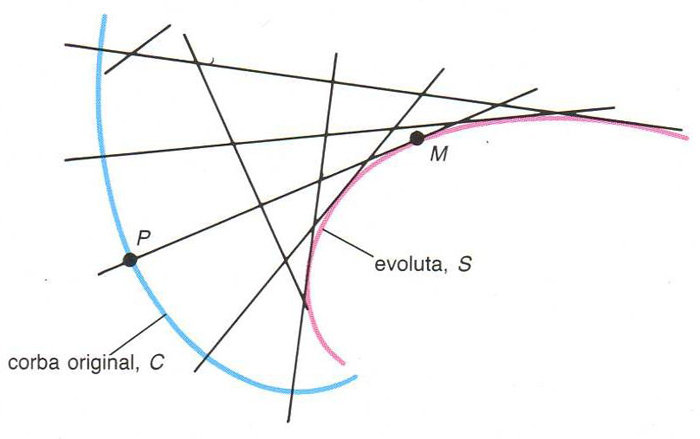
La corba S és l’evoluta de C
© fototeca.cat
Matemàtiques
Donada una corba plana C
, lloc geomètric dels centres de curvatura de C
.
És l'envolupant S de les normals a la corba C així, una normal en el punt P a C és tangent a l’evoluta i el punt de tangència M és el centre de curvatura de C en el punt P Si S és l’evoluta de C , C és una evolvent de S L’evoluta d’un cercle es redueix a un punt
Muḥammad ibn Mūsà al-Ḫwārizmī
Astronomia
Matemàtiques
Astrònom i matemàtic persa.
Adscrit a la cort d’al-Ma‘mūn a Bagdad, escriví tota la seva aportació coneguda en àrab La seva obra, Algorithmi de numero indorum , conservada només en versió llatina, contribuí a la difusió del sistema numèric actual Desenvolupà considerablement el càlcul algèbric el terme “àlgebra” i els seus derivats provenen del seu Kitāb al-muḫtasar fi ḫišab al-ǧabr wa-I-muqābala , sobretot la teoria de les equacions de segon grau, i també és autor de tractats de geometria, d’unes taules astronòmiques perfeccionades per al-Maǧritī i de diversos escrits sobre l’astrolabi Els termes “algorisme” i “…
esfera
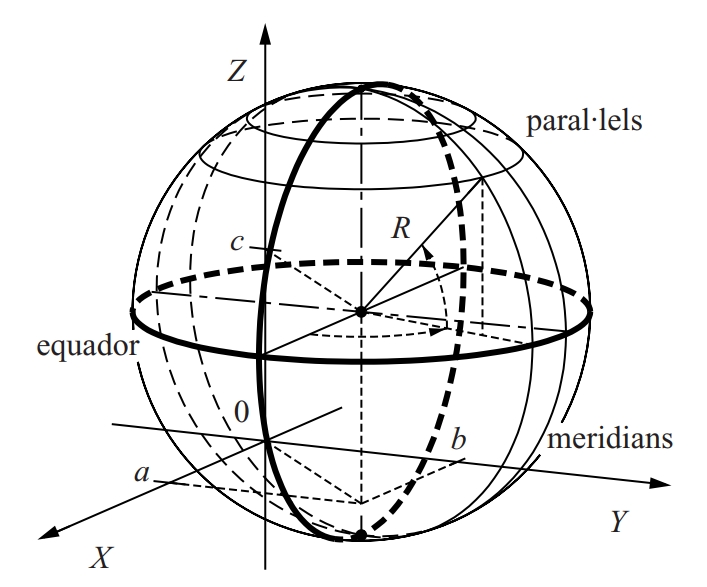
Esfera de centre (a, b, c) i radi R
Matemàtiques
Figura espacial generada per la rotació d’un cercle al voltant d’un dels seus diàmetres.
Es tracta d’una quàdrica amb equació cartesiana x – a 2 + y – b 2 + z – c 2 = R 2 si el centre és el punt a , b , c i el radi és R El seu volum val i la seva superfície S = 4 π R 2
evolvent
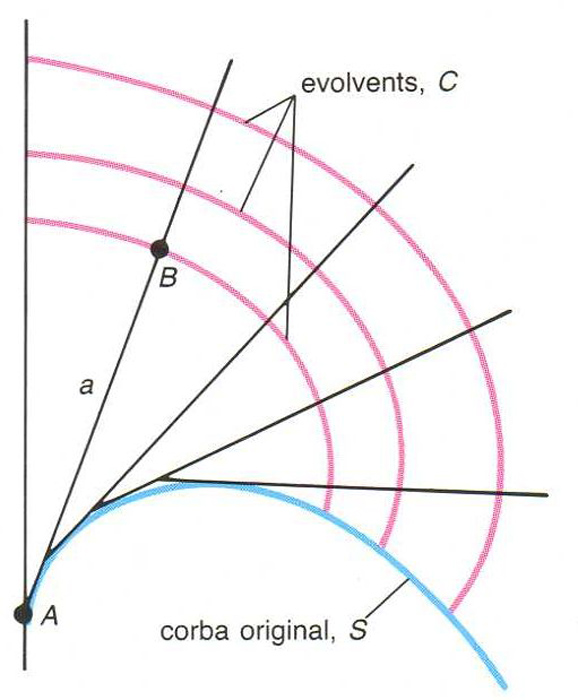
Les corbes C són les evovlents de S
© fototeca.cat
Matemàtiques
Donada una corba S
, cadascuna de les corbes ortogonals a les tangents de S
.
Si C és una envolvent de S , S és l'evoluta C Donada la corba S , hom pot generar una evolvent tot fixant una tangent a S en un punt de tangència A , limitant-ne la seva longitud a i anant-la enrotllant a la corba, de manera que el punt extrem B determina una evolvent Les diferents longituds a determinen les diferents evolvents
complement d’una part d’un conjunt
Matemàtiques
Donada una part A
d’un conjunt C, A ⊂C,
subconjunt de C
format pels elements de C
que no pertanyen a A
; és representat per CA
.
De manera menys precisa, hom pot definir també el complement d’un conjunt qualsevol C , com el complement del conjunt respecte al conjunt universal format per tots els possibles elements de tots els possibles conjunts, és a dir, el complement de C és el conjunt C' tal que C ∪ C' = U i C ∩ C' = ∅on U és el conjunt universal
funció d’elecció
Matemàtiques
Donat un conjunt no buit C, funció f:℘(C)→C, on
℘(C) és el conjunt de les parts de C, que assigna a cada part X no
buida de C un dels seus elements: f(X)∈X.
L' axioma d’elecció afirma que per a tot conjunt no buit C existeix almenys una funció d’elecció
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina