Resultats de la cerca
Es mostren 11 resultats
homologia
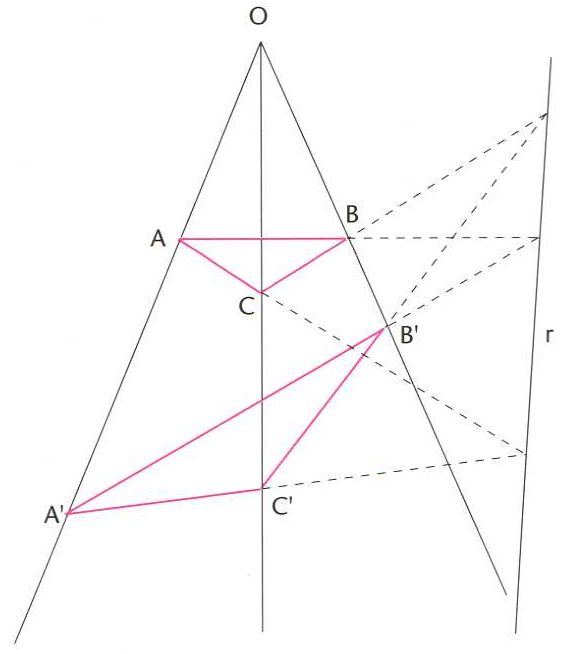
Trasformació per homologia d’un triangle ABC en A'B'C’ (O, centre de l’homologia; r, eix de l’homologia)
© Fototeca.cat
Matemàtiques
Teoria que estudia les transformacions entre espais topològics que conserven certes estructures algèbriques definides en cada espai.
Iṣḥaq ben Mošé Elí ha-Sefardí
Literatura
Matemàtiques
Judaisme
Autor jueu del qual es conserven, en hebreu, escrits després de l’expulsió de l’any 1492, dos llibres de matemàtiques elementals.
semblança
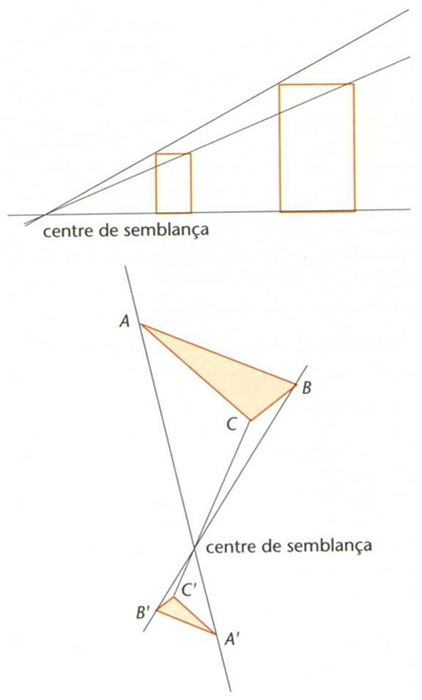
Dues semblances directes
© Fototeca.cat
Matemàtiques
Transformació geomètrica T de ℝn en ℝn tal que la distància entre les imatges de dos punts qualssevol és igual a la distància entre aquests dos punts multiplicada per una quantitat constant positiva dita raó de la semblança.
És a dir, d T x, T y = k, d x, y Dues figures són anomenades semblants si hi ha una semblança que transforma l’una en l’altra Les semblances conserven la forma de les figures però en canvien la grandària, eixamplant-la o reduint-la segons que la raó sigui respectivament major o menor que 1 Les semblances de raó 1 són dites isometries o moviments rígids , els quals són sempre el resultat de compondre una translació amb una transformació lineal ortogonal que conserva els angles Les homotècies són exemples típics de semblances Tota semblança és el resultat d’aplicar successivament…
moviment
Matemàtiques
Aplicació d’un espai mètric en ell mateix que conserva la distància.
Actualment hom tendeix a anomenar-lo isometria El conjunt de moviments definits sobre un espai, amb l’operació de composició o producte de moviments, constitueix un grup En particular, és interessant l’estudi dels moviments al pla i a l’espai ordinaris El grup dels moviments del pla és generat per les simetries axials, és a dir, tot moviment del pla pot ésser descompost en producte d’un cert nombre de simetries axials Els de nombre parell són anomenats moviments directes , conserven el sentit del pla i són un subgrup del grup de moviments els altres són anomenats moviments…
transposició
Matemàtiques
En una matriu, canvi de les files per les columnes.
Així, la matriu es transforma per transposició en El determinant d’una matriu quadrada és invariant per transposició Una matriu en què la inversa és igual a la transposada, és anomenada ortogonal aquestes matrius representen els moviments lineals que conserven distàncies, angles i productes escalars
homotècia
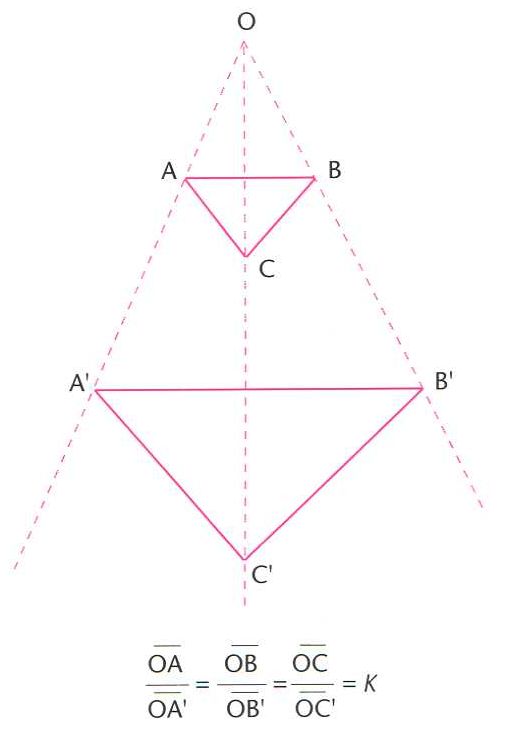
Homotècia, transformació homotètica d’un triangle ABC (O, centre de l’homotècia; k, raó d’homotècia)
© Fototeca.cat
Matemàtiques
Transformació geomètrica del pla o de l’espai que compleix aquestes dues condicions.
Qualsevol punt A i la seva imatge A' són alineats amb un punt fix O anomenat centre d’homotècia , i els segments compleixen la relació k essent, per a cada homotècia, una constant real anomenada raó de l’homotècia Les homotècies transformen rectes en rectes, circumferències en circumferències i conserven els angles
equacions d’Einstein-Lorentz
Matemàtiques
Si hom considera dos observadors que es mouen amb velocitat relativa v en la direcció d’un eix comú que hom pren com a eix de les ics, la posició i el temps en què s’esdevé un succés P seran amidats per un observador en funció de les coordenades x, y, z i del temps t i, per l’altre, en funció d'x', y', z' i t', dependents del seu sistema referencial.
Les equacions d’Einstein-Lorentz estableixen el lligam que hi ha entre aquestes dues quaternes de nombres i són que admeten la transformació inversa que hom obté canviant x , y , z , t per x ', y' , z' , t' i canviant el signe de v És d’interès observar que 1/ c = 0 proporciona la transformació clàssica o galileana Dit altrament, si v és força negligible davant de la velocitat c de la llum, aleshores la transformació d’Einstein-Lorentz esdevé la transformació de la mecànica clàssica Cal remarcar, finalment, que les transformacions d’Einstein-Lorentz conserven la forma de l’…
translació
Matemàtiques
Transformació geomètrica que a cada punt M
del pla n’hi associa un altre M’
de manera que el vector de manera que el vector
sigui un representant d’un vector lliure
prefixat, anomenat vector de la translació
Les translacions són isometries que en el pla conserven el sentit de les rotacions i en l’espai el caràcter dels tríedres, no tenen punts dobles i en les quals les rectes i els plans parallels al vector de translació són invariants El conjunt de totes les translacions del pla o de l’espai formen un grup commutatiu amb l’operació composició, el qual és isomorf al grup additiu dels vectors lliures ordinaris associats al pla o a l’espai considerat Si és el vector característic d’una translació, el punt transformat d’un punt M x 1 ,x 2 ,x 3 és el punt M' x' 1 ,x' 2 ,x' 3 , les…
Āryabhaṭa
Astronomia
Matemàtiques
Matemàtic i astrònom indi de l’era Gupta.
Un dels més grans matemàtics de l’Índia i el primer científic d’aquest país del qual es conserven escrits Autor del tractat Āryabhatṭiyā 499, dividit en quatre parts A la primera proposa una notació dels nombres mitjançant síllabes A les altres tres parts tracta temes d’astronomia, entre els quals una teoria dels epicicles, i és el primer a parlar de la rotació de la terra entorn del seu eix Els seus principals treballs de matemàtiques són l’extracció d’arrels quadrades i cúbiques, on utilitza el sistema decimal amb el zero, la suma de progressions aritmètiques, la resolució d’…
transformació
Matemàtiques
Aplicació bijectiva d’un conjunt en un altre o en ell mateix.
El conjunt de les transformacions d’un conjunt en ell mateix té estructura de grup respecte a la composició de transformacions la composició en el sentit d’aplicar successivament de manera ordenada dues transformacions és anomenada també producte Segons la definició de Felix Klein, la geometria és l’estudi de les nocions invariants per a un grup de transformacions geometria Com a exemples de transformacions en el pla poden ésser esmentades les rotacions, les simetries axials, les translacions, etc i en l’espai, les simetries respecte a un eix o a un pla, les rotacions axials, etc Segons les…