Resultats de la cerca
Es mostren 26 resultats
integració
Matemàtiques
Càlcul d’una integral.
Per a calcular integrals indefinides són útils, sovint, el mètode d’integració per substitució i el mètode d’integració per parts Segons el primer, hom fa x = φ t , i substitueix aquest valor a la integral ∫ f x dx = ∫fϕ t ϕ´ t dt , a fi de resoldre aquesta darrera més fàcilment El mètode d’integració per parts es basa en la relació → u dv = uv - que sigui de fàcil resolució Trobada la funció primitiva F x , la solució és ∫ f x dx = F x + C , on C és una constant La regla de Barrow proporciona un mètode general per a calcular integrals definides a partir de les…
ordenat | ordenada
Matemàtiques
Dit del conjunt que té definida una relació d’ordre.
Un grup G , + és dit ordenat per la relació d’ordre ≤, si es compleix la propietat d’isotonia o compatibilitat de l’operació + respecte a l’ordre ≤, és a dir, si per tot x, y, z , de G, x ≤ y implica x + z ≤y + z i z + x ≤ z + y Un anell o un espai vectorial són dits ordenats si aquesta llei d’isotonia és vàlida per a totes les operacions que hi són definides
convergència
Matemàtiques
Qualitat de convergent.
En el cas d’una successió de funcions hom pot parlar de convergència en diferents sentits, segons la topologia donada en el conjunt de funcions a considerar així, hi ha la convergència puntual una successió f n tendeix a f si, per a tot x on les f n estan definides, f n x té límit f x la convergència uniforme f n convergeix uniformement a f si, per a tot ε> 0, es dona un N tal, que n> N implica | f n x - f x |
teorema de Bonnet
Matemàtiques
Teorema segons el qual els coeficients de les formes fonamentals d’una superfície determinen localment la parametrització de la superfície, llevat de composició amb transformacions ortogonals pròpies i translacions.
Concretament, si E , F , G , e , f , g són funcions diferenciables definides en un obert V ⊂ ℝ 2 , amb E > 0, G > 0 i EG – F 2 > 0 tals que satisfan les equacions de compatibilitat de Gauss i de Mainardi-Codazzi, aleshores per a cada q ∈ V existeix un entorn U ⊂ V de q i un difeomorfisme x U → x U ⊂ ℝ 3 tal que la superfície regular x U ⊂ ℝ 3 té E , F , G , e , f , g per coeficients en les seves formes fonamentals Amés, si U és connex i x’ U → x’ U ⊂ ℝ 3 és un altre difeomorfisme que satisfà les mateixes condicions, aleshores existeix una translació T i una…
funcions d’Hermite
Matemàtiques
Funcions en ℝ definides per
on Hn(x) és un polinomi d'Hermite.
transformació
Matemàtiques
Aplicació bijectiva d’un conjunt en un altre o en ell mateix.
El conjunt de les transformacions d’un conjunt en ell mateix té estructura de grup respecte a la composició de transformacions la composició en el sentit d’aplicar successivament de manera ordenada dues transformacions és anomenada també producte Segons la definició de Felix Klein, la geometria és l’estudi de les nocions invariants per a un grup de transformacions geometria Com a exemples de transformacions en el pla poden ésser esmentades les rotacions, les simetries axials, les translacions, etc i en l’espai, les simetries respecte a un eix o a un pla, les rotacions axials, etc Segons les…
homologia
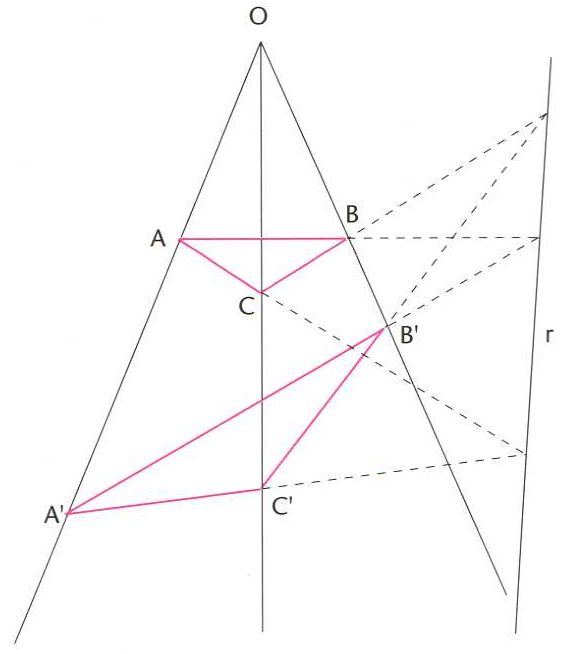
Trasformació per homologia d’un triangle ABC en A'B'C’ (O, centre de l’homologia; r, eix de l’homologia)
© Fototeca.cat
Matemàtiques
Teoria que estudia les transformacions entre espais topològics que conserven certes estructures algèbriques definides en cada espai.
atzar
Matemàtiques
Conjunt de causes inconegudes que produeixen un efecte no previsible; un fenomen és atribuïble a l’atzar, o és fortuït o és aleatori, quan no és ni inevitable ni impossible.
Una característica important d’aquests fenòmens és que llur realització depèn d’un conjunt de condicions massa complexes per a poder-les conèixer i estudiar totes Un esdeveniment que apareix inevitablement quan es produeix un conjunt de condicions és un esdeveniment cert respecte a aquestes hom anomena impossibles els que mai no poden aparèixer Els esdeveniments fortuïts són els que tant poden donar-se com no donar-se si es realitzen les condicions és a dir, si aquestes no reflecteixen del tot les condicions necessàries i suficients perquè es realitzi l’esdeveniment, i es tracta…
recursiu | recursiva
Matemàtiques
Dit de les funcions que són definides per recurrència (definició per recurrència), com és el cas de la funció factorial.
relació
Matemàtiques
Lligam entre diversos elements d’un conjunt.
Per tal de precisar aquesta idea intuïtiva, hom defineix la relació com a qualsevol subconjunt d’un producte cartesià del conjunt amb ell mateix és a dir, que els elements són relacionats si formen un element del subconjunt En general, en una relació intervé un nombre determinat d’elements n així, una relació d’ordre entre els elements és un subconjunt del producte de n conjunts A El tipus de relació més freqüent és aquella en què n = 2, anomenada relació binària , que és un subconjunt de A × A Si els dos elements són a i b , hom diu que a R b , o que a és relacionat amb b —o sia, que a,b…