Resultats de la cerca
Es mostren 35 resultats
rotació
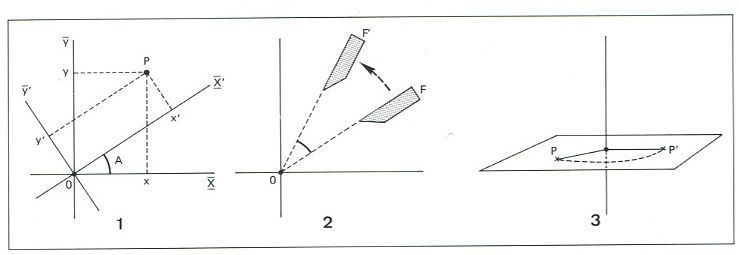
rotació: 1, d'eixos; 2, al voltant d'un punt0; 3, al voltant d'un eix
Matemàtiques
Transformació geomètrica que constitueix un dels moviments rígids del pla o de l’espai i que conserva les distàncies (mides i forma) i l’orientació de les figures sobre les quals és aplicada.
En el pla hom considera la rotació al voltant d’un punt fix que correspon a moviments rígids circulars de centre al punt donat En l’espai hom considera la rotació al voltant d’una línia , en la qual qualsevol punt d’una figura es mou en sentit circular al voltant de la línia donada eix de rotació, en un pla perpendicular a aquesta i que passa pel punt donat Una rotació d’eixos correspon a una rotació que deixa fix l’origen de coordenades Aquestes rotacions permeten de passar d’un sistema de referència a un altre que pot ésser més adequat per a l’estudi d’un problema geomètric…
hiperboloide
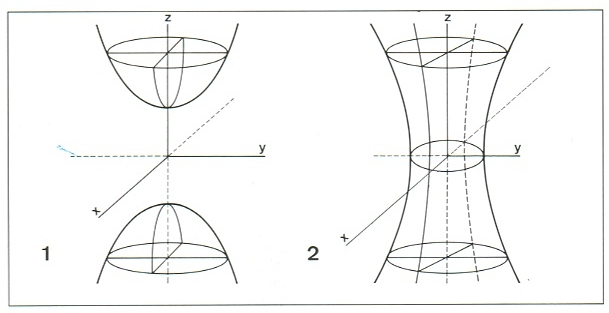
hiperboloide 1, de dues fulles; 2, d'una fulla
Matemàtiques
Quàdrica que, respecte als seus tres eixos de simetria, té per equació (x2/a2) + (y2/b2) - (z2/c2) = ±1.
Entre les seves seccions planes, n'hi ha que són hipèrboles Quan el signe del segon membre és +, l’hiperboloide és anomenat d’una fulla o hiperbòlic quan és -, l’hiperboloide és anomenat de dues fulles o ellíptic Un hiperboloide és anomenat de revolució quan hom el pot considerar generat per la rotació d’una hipèrbola entorn d’un dels seus eixos de simetria
sistema de coordenades
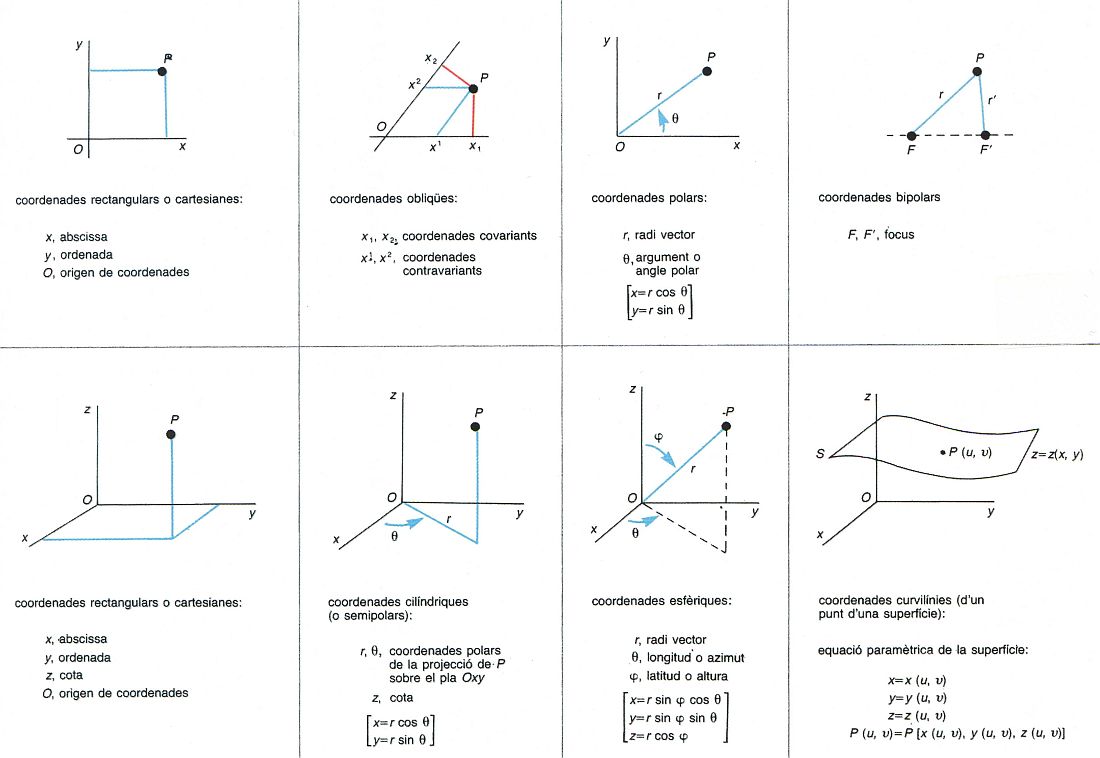
Sistemes de coordenades matemàtiques: coordenades d’un punt del pla (superior) i d’un punt de l’espai (inferior)
©
Matemàtiques
En un cert domini X, conjunt de funcions tal, que els valors en un punt el determinen, de manera que mitjançant un sistema de coordenades cada punt és definit per un conjunt de nombres, que són les coordenades del punt.
Segons els casos les funcions d’un sistema han de complir certes condicions Així, en el pla, un sistema de coordenades lineal consisteix en dues funcions lineals independents Els eixos del sistema són les rectes que corresponen al valor zero de cadascuna de les funcions La intersecció dels dos eixos és l' origen de coordenades Si els eixos són perpendiculars, el sistema és rectangular i les coordenades són rectangulars o cartesianes Si els eixos són oblics, les coordenades són obliqües o rectilínies obliqües En aquest cas, hom pot…
axonometria
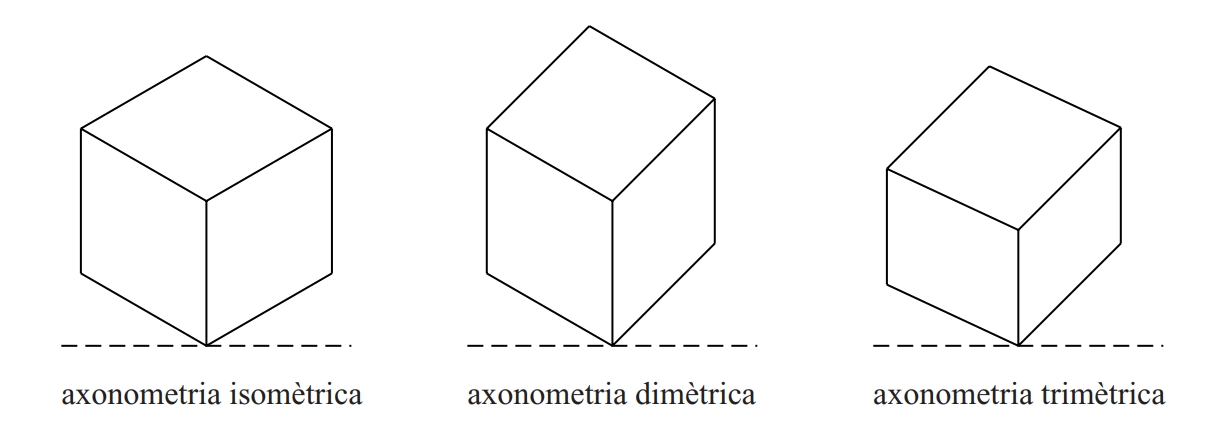
axonometria
© Fototeca.cat
Matemàtiques
Mètode de representació de les figures de l’espai.
En aquest sistema hom pren un tríedre trirectangle com a referència i determina cada punt de l’espai per les seves projeccions ortogonals damunt els plans del tríedre Després hom projecta sobre el pla del dibuix la figura formada pel tríedre, el punt i les seves projeccions sobre els plans del tríedre És útil, per a fixar bé la posició de la figura a l’espai, de dibuixar les interseccions dels plans del tríedre amb el pla de dibuix Aquestes rectes d’intersecció són anomenades traces Projecció axonomètrica d’un cub © Fototecacat Per a determinar les projeccions d’un punt convé de graduar els…
estereografia
Matemàtiques
Mètode per a representar els sòlids sobre un pla mitjançant projeccions
.
També anomenada projecció estereogràfica, s’utilitza principalment en cristallografia per a representar les cares i els eixos dels cristalls, i en geologia estructural per a representar i analitzar espacialment elements estructurals tals com superfícies i eixos de plecs, foliacions, etc
moviment
Matemàtiques
Aplicació d’un espai mètric en ell mateix que conserva la distància.
Actualment hom tendeix a anomenar-lo isometria El conjunt de moviments definits sobre un espai, amb l’operació de composició o producte de moviments, constitueix un grup En particular, és interessant l’estudi dels moviments al pla i a l’espai ordinaris El grup dels moviments del pla és generat per les simetries axials, és a dir, tot moviment del pla pot ésser descompost en producte d’un cert nombre de simetries axials Els de nombre parell són anomenats moviments directes , conserven el sentit del pla i són un subgrup del grup de moviments els altres són anomenats moviments inversos Dins el…
ortoròmbic | ortoròmbica
Louis Poinsot
Matemàtiques
Matemàtic francès.
Fou professor a l’École Polytechnique i s’especialitzà en mecànica Desenvolupà la teoria dels parells i del moviment d’un cos sòlid al voltant d’un punt fix, on introduí el concepte d’inèrcia a la rotació al voltant de certs eixos característics Publicà Éléments de statique 1803 i Nouvelle théorie de la rotation des corps 1832
coordenades cartesianes
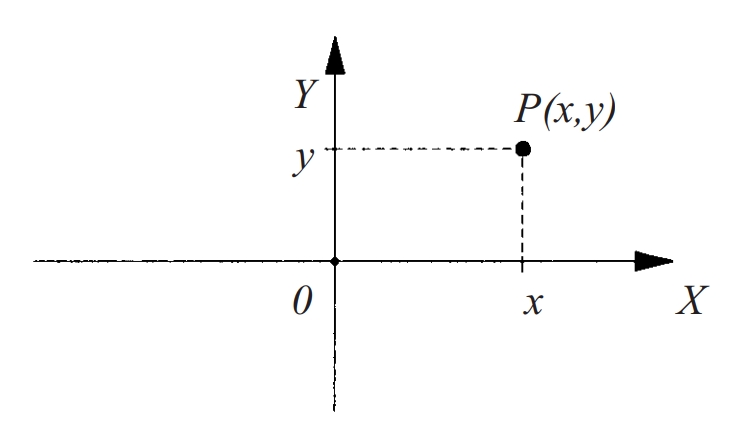
coordenades cartesianes al pla
Matemàtiques
En un espai euclidià, coordenades afins respecte d’una referència afí.
En el cas d’una referència, es diu que les coordenades són cartesianes rectangulars Així, tot punt del pla espai P s’identifica amb les seves coordenades x , y x , y , z on cada coordenada representa la projecció de P en l’eix corresponent d’acord amb la direcció dels altres eixos També s’usen referències no ortogonals coordenades cartesianes a l’espai
centre
Matemàtiques
Punt on es tallen els eixos de simetria d’una figura geomètrica.