Resultats de la cerca
Es mostren 10 resultats
equacions d’Einstein-Lorentz
Matemàtiques
Si hom considera dos observadors que es mouen amb velocitat relativa v en la direcció d’un eix comú que hom pren com a eix de les ics, la posició i el temps en què s’esdevé un succés P seran amidats per un observador en funció de les coordenades x, y, z i del temps t i, per l’altre, en funció d'x', y', z' i t', dependents del seu sistema referencial.
Les equacions d’Einstein-Lorentz estableixen el lligam que hi ha entre aquestes dues quaternes de nombres i són que admeten la transformació inversa que hom obté canviant x , y , z , t per x ', y' , z' , t' i canviant el signe de v És d’interès observar que 1/ c = 0 proporciona la transformació clàssica o galileana Dit altrament, si v és força negligible davant de la velocitat c de la llum, aleshores la transformació d’Einstein-Lorentz esdevé la transformació de la mecànica clàssica Cal remarcar, finalment, que les transformacions d’Einstein-Lorentz conserven la forma de l’…
funció implícita
Matemàtiques
Donada una funció f:ℝ2→ℝ, funció f:ℝ→ℝque assigna a un x∈ℝ el valor (o valors) y que satisfà f(x,y)=0, cas que existeixi.
Si d’aquesta equació hom pot expressar explícitament y en funció de x la funció esdevé explícita Per exemple, donada la funció f x,y =4 x 2 + xy + y 6 , l’equació 4 x 2 + xy + y 6 =0 defineix una funció implícita f x
el·lipsoide
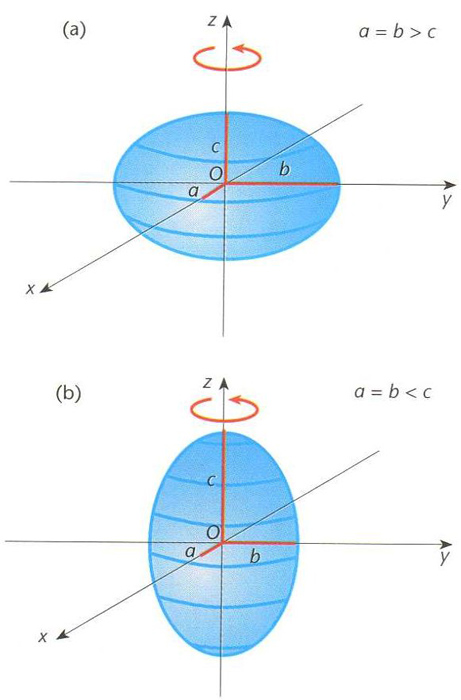
El·lipsoide aplatat (a) i allargat (b) obtinguts per rotació d’una el·lipse, prenent com a eix de la rotació el que conté, en el primer cas, el semieix menor d’aquesta el·lipse i, en el segon, el semieix major
© Fototeca.cat
Matemàtiques
Superfície de segon grau o quàdrica amb centre l’equació de la qual és (
x 2
/a 2
)+(
y 2
/b 2
)+(
z 2
/c 2
)=1 si els eixos de coordenades són els propis de la quàdrica.
Una ellipse que giri al voltant del seu eix menor determina un ellipsoide aplatat , anomenat també esferoide oblat i una ellipse que giri al voltant del seu eix major determina un ellipsoide allargat , anomenat també esferoide prolat Quan a=b=c=r l’ellipsoide esdevé una esfera de radi r
àlgebra
Matemàtiques
Anell B que esdevé un A-mòdul a causa d’un homomorfisme entre un anell A i B.
Tot anell és sempre una ℤ-àlgebra, en què ℤ denota l’anell dels nombres enters
funció multiforme
Matemàtiques
Funció que assigna diverses imatges a cada element del domini de definició.
En són exemple les funcions trigonomètriques inverses arc sin1 = {π/2, π/2+2π, π/2+4π,,π/2+2 n π,} Les funcions multiformes no són, en el sentit estricte del terme funcions , sinó correspondències Una funció multiforme esdevé una funció quan hom n'escull una branca o determinació per exemple, la funció Arc sin x és la branca de la funció multiforme arc sin x definida en restringir a 0,2π el recorregut d’aquesta
integral impròpia
Matemàtiques
Integral que, a causa de no ésser definida o fitada, la funció a integrar, en algun punt del seu domini de definició, no és calculable directament.
Així, quan la funció f no és definida o fitada a un punt c del seu domini de definició a,b , hom defineix la integral impròpia de f en a,b per si aquests dos límits existeixen, la integral és anomenada convergent i, en cas contrari, divergent Un altre cas d’integral impròpia s’esdevé quan un dels límits d’integració és infinit la integral és definida aleshores, segons el cas, per Les integrals impròpies són també anomenades integrals generalitzades
binomi de Newton
Matemàtiques
Fórmula per a calcular la potència enèsima d’un binomi, anomenada també teorema del binomi.
En el cas que l’exponent n del binomi sigui un nombre natural, la fórmula pot ésser demostrada per inducció, i la seva expressió és on els coeficients n k , anomenats coeficients binomials , són donats per la fórmula Aquesta expressió, que ja utilitzà NTartaglia, fou ampliada per INewton en el cas d’exponents negatius i fraccionaris i per LEuler en el cas d’exponents irracionals En el cas, però, que l’exponent n no sigui un nombre natural, l’anterior expressió esdevé una sèrie infinita i, per tant, només té sentit quan la sèrie és convergent, cosa que imposa certes limitacions…
discontinuïtat
Discontinuïtat d’una funció: (a) discontinuitat evitable en x = 0, amb valor veritable y(0) = 0; (b) discontinuïtat de primera espècie infinita en x = 0, amb salt -2; (c) discontinuïtat de primera espècie infinita amb un punt d’infinit en x = 0; i (e) discontinuïtat de segona espècie finita en x = 0, per inexistència d’ambdós límits laterals quan x 0
© Fototeca.cat
Matemàtiques
Manca de continuïtat d’una funció en un punt o en un conjunt de punts, els quals són anomenats, per extensió, les discontinuïtats de la funció.
Atès que una funció f x és contínua en un punt a si i només si existeix i és igual a f a , la funció f x és discontínua en a si i només si no se satisfà alguna d’aquestes dues condicions, la qual cosa s’esdevé en els següents casos En primer lloc, pot passar que existeixi però que f a no existeixi f no sigui definida a a , o bé que aleshores, a és una discontinuïtat evitable , i la discontinuïtat és evitada redefinint el valor de f x al punt a tot assignant-li el valor el qual és anomenat valor veritable de f x en a En segon lloc, pot ocórrer que no existeixi…
René du Perron Descartes
Filosofia
Matemàtiques
Filòsof i científic francès.
Conegut també amb el nom llatinitzat de Cartesius , és considerat generalment com el pare de la filosofia moderna Fill d’un conseller del parlament de Bretanya, fou educat al collegi dels jesuïtes de La Flèche, i es llicencià en dret a Poitiers Desitjós de conèixer “el llibre del món”, el 1618 començà un llarg període de viatges, primerament com a soldat i després com a particular Per assegurar-se una vida tranquilla de meditació i estudi, el 1628 es retirà a Holanda, on romangué més de vint anys, fins que, acceptant la invitació de la reina Cristina de Suècia, es traslladà a Estocolm, on…
teoria de la computació
Matemàtiques
Branca de les matemàtiques que estudia problemes de decidibilitat.
Com és usual en la història de les matemàtiques, té orígens aparentment molt diferents que finalment conflueixen i permeten d’establir el que esdevé una teoria enormement potent i irrenunciable Cal remarcar-ne el problema diofàntic plantejat per David Hilbert l’any 1900, i el problema de les paraules que sorgí en el món de la topologia algèbrica Es tracta de dos problemes típics de decidibilitat és a dir, aquells en què cal disposar d’un mètode que permeti de decidir una o altra de dues opcions atesa una equació diofàntica, té solució, són equivalents dues paraules donades per endavant L’any…