Resultats de la cerca
Es mostren 12 resultats
intuïcionisme
Matemàtiques
Corrent del pensament matemàtic, nascut a la segona meitat del s XIX.
Propugna que la matemàtica és l’estudi d’uns tipus de construccions mentals en les quals els objectes que hom maneja han d’ésser definits donant un criteri que en permeti la construcció i on el llenguatge emprat, sigui ordinari o simbòlic, només és un instrument auxiliar i no una part essencial de les construccions formalisme Hom accepta que la matemàtica intuïcionista és formada de tot allò que és conseqüència segons les normes de la lògica intuïcionista de la construcció de la successió dels nombres naturals ℕ, de la qual resulten evidents els axiomes de Peano base de la…
Diofant d’Alexandria
Matemàtiques
Matemàtic grec.
Els seus escrits sobre àlgebra, amb un estil d’exposició marcadament analític que el vincula estretament amb els treballs dels babilonis, contribuïren de forma essencial al perfeccionament de la notació algèbrica i a l’establiment de noves vies d’investigació En la seva obra cabdal, Aritmètica , estudià una àmplia sèrie de problemes numèrics limitant-se, en general, a trobar-hi solucions particulars mitjançant algun mètode de càlcul i admetent només com a solucions els nombres enters i racionals positius La seva obra influí en el posterior desenvolupament de la geometria…
Yves Meyer
Matemàtiques
Matemàtic francès.
Graduat en matemàtiques per l’Escola Normal Superior ENS de París 1957, obtingué el doctorat per la Universitat d’Estrasburg el 1966 Ha desenvolupat la seva trajectòria docent i de recerca successivament a l’escola militar Prytanée 1960-63, la Universitat d’Estrasburg 1963-66, la Universitat de París-Sud 1966-80, l’École Polytechnique 1980-86, la Universitat de París-Dauphiné 1985-95 i al centre de matemàtiques CMLA de l’ENS fins a la jubilació 2008, d’on fou nomenat professor emèrit Ha fet aportacions a la teoria dels nombres i, especialment, a l’anàlisi harmònica, camp en el qual, en…
fractal
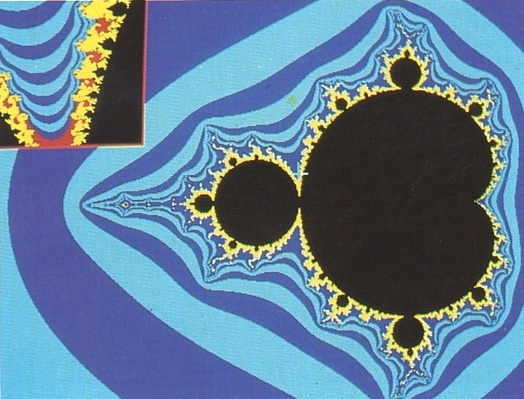
fractal Conjunt de Mandelbrot i un detall (corresponent al punt marcat per una creu blanca) [imatge obtinguda per ordinador al Departament d’Informàtica de la Universitat Autònoma de Barcelona]
Matemàtiques
Model matemàtic o objecte real que manté la seva forma essencial, fragmentada i irregular, tot i variant l’escala d’observació.
Les primeres fractals corbes de Von Koch, Peano, Sierpiński, etc aparegueren entre el 1875 i el 1925 com a contraexemples als intents de formalització de l’actual matemàtica Benoît Mandelbrot, els anys setanta, descobrí que aquests models serveixen per a representar la realitat Basant-se en els conceptes d’homotècia interna i de dimensió en el sentit de Hausdorff-Besikovič 1919, Mandelbrot definí les bases de la geometria fractal, que permet de modelitzar fenòmens com les turbulències, el cabal dels rius, el soroll blanc, la distribució de les galàxies, les estructures geològiques, etc, tots…
axiomàtica
Filosofia
Matemàtiques
Conjunt d’axiomes no contradictoris i independents que es formulen per a poder desenvolupar una teoria d’una manera deductiva lògicament correcta.
La matèria que es presta més a ésser tractada en forma axiomàtica és la matemàtica, bé que el mètode és aplicable al desenvolupament teòric d’altres ciències física, economia, estadística, etc Cada una de les proposicions admeses com a base de l’estudi axiomàtic d’una teoria és anomenada axioma o postulat aquests dos mots, en matemàtiques, són considerats sinònims Un sistema de postulats és un conjunt de proposicions breus que tradueixen les veritats fonamentals de la teoria a la qual serveixen de base És desitjable que els postulats d’un sistema siguin simples , és a dir, que…
discontinuïtat
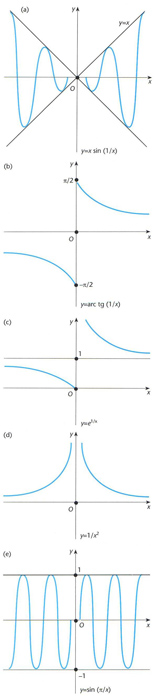
Discontinuïtat d’una funció: (a) discontinuitat evitable en x = 0, amb valor veritable y(0) = 0; (b) discontinuïtat de primera espècie infinita en x = 0, amb salt -2; (c) discontinuïtat de primera espècie infinita amb un punt d’infinit en x = 0; i (e) discontinuïtat de segona espècie finita en x = 0, per inexistència d’ambdós límits laterals quan x 0
© Fototeca.cat
Matemàtiques
Manca de continuïtat d’una funció en un punt o en un conjunt de punts, els quals són anomenats, per extensió, les discontinuïtats de la funció.
Atès que una funció f x és contínua en un punt a si i només si existeix i és igual a f a , la funció f x és discontínua en a si i només si no se satisfà alguna d’aquestes dues condicions, la qual cosa s’esdevé en els següents casos En primer lloc, pot passar que existeixi però que f a no existeixi f no sigui definida a a , o bé que aleshores, a és una discontinuïtat evitable , i la discontinuïtat és evitada redefinint el valor de f x al punt a tot assignant-li el valor el qual és anomenat valor veritable de f x en a En segon lloc, pot ocórrer que no existeixi aleshores, a és una…
àbac

Àbac xinès
© Fototeca.cat
Matemàtiques
Aparell simple de càlcul digital que permet de fer totes les operacions aritmètiques bàsiques.
Consisteix, normalment, en un tauler o marc proveït de filferros parallels, amb boles foradades que corren al llarg d’aquests Cada enfilall representa un lloc decimal unitats, desenes, centenes, etc, i llur nombre pot ésser variable Les operacions s’efectuen canviant de posició unes boles en relació amb les altres, i, amb una manipulació complicada, hom pot aconseguir fins l’extracció d’arrels L’àbac fou usat a l’antic Egipte i probablement a Babilònia, d’on passà a Grècia i a Roma L’àbac romà consistia en una taula amb diverses ranures paralleles per on hom feia córrer pedres o botons, amb…
subespai
Matemàtiques
Qualsevol subconjunt no buit F d’un espai vectorial E (sobre un cos K) tal, que és estable per a les dues lleis de E i que, proveït d’aquestes lleis induïdes, és també un espai vectorial (sobre K).
En l’espai vectorial de tres dimensions ℝ 3 els subespais són el mateix espai, l’origen de coordenades i totes les rectes i els plans que passen per l’origen F és un subespai de E si, donats qualssevol x , y de F i λ de K , aleshores la combinació lineal x ,-λ y pertany a F Tota família de vectors determina l’anomenada envolupant lineal , o mínim subespai, que els conté La intersecció M ∩ N de dos subespais M i N és un subespai, però la reunió M ∪ N no ho és en general La suma M + N definida per a tots els vectors que són suma d’un element de M i un de N és el mínim subespai que conté la…
problema
Matemàtiques
Tota qüestió en què partint d’unes dades conegudes cal arribar a uns resultats.
El resultat d’un problema pot ésser de natura molt diversa cal distingir, dins la matemàtica, els problemes de calcular, els problemes de construir i els problemes de demostrar En els problemes de calcular , és possible que per analogia amb altres problemes ja coneguts hom pugui aplicar unes regles que donen directament la solució, que pot constar d’un o més nombres Quan aquestes regles no són fàcils de descobrir hom recorre a expressar algèbricament les condicions de l’enunciat, és a dir, expressar per mitjà d’equacions les relacions entre les dades i les incògnites del problema si aquestes…
tensor
Física
Matemàtiques
Objecte abstracte que posseeix un determinat sistema de components en cada sistema referencial que hom consideri i tal que, sota transformacions de coordenades, les seves components variïn d’acord amb una transformació predeterminada.
Si E és un espai vectorial de dimensió n sobre un cos algèbric K , hom defineix el tensor covariant d’ordre r com una aplicació T r definida en E x E x r x E = E r , i per a valors en K tal que és lineal en cada component, és a dir, que per a i = 1, 2, 3, , r es compleix a T r x 1 , , x i + y i , , x r = T r x ₁ , , x i ,, x r + T r x 1 , , y i , , x r b T r x ₁ , , λ x i , , x r = λ T r x ₁ , , x i , , x r Els tensors covariants d’ordre 1 formen l’espai E *, anomenat dual de E , és a dir, el conjunt d’aplicacions lineals de E en K E * és, alhora, un espai vectorial de dimensió…