Resultats de la cerca
Es mostren 12 resultats
Abū-l-Ḥusayn al-Rāzī
Astronomia
Matemàtiques
Matemàtic i astrònom àrab.
És autor del Kitāb al-kawākib al-ṯābita al-muṣawwar ‘Llibre illustrat dels estels fixos’, on donà a conèixer diversos estels ignorats per Ptolemeu i corregí dades errònies d’aquest
punt fix
Matemàtiques
En una aplicació f, punt x que verifica la condició f(x) = x.
També és anomenat punt doble Per exemple, el centre de simetria és un punt doble en la simetria central Brouwer ha demostrat l’anomenat teorema del punt fix , segons el qual tota aplicació contínua en una esfera n -dimensional amb ng 2 té un punt fix El teorema té com a conseqüència que la major part de les deformacions físiques tinguin punts fixos
equipol·lència
Matemàtiques
Relació d’equivalència entre vectors fixos de l’espai euclidià.
Dos vectors són equipollents si existeix una translació que transforma l’un en l’altre Les classes de vectors equipollents són anomenades vectors lliures vector
hipèrbole
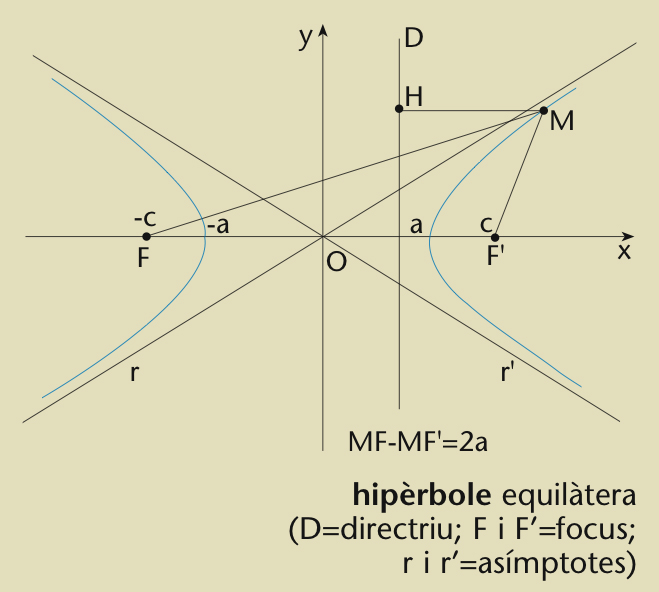
Hipèrbole equilàtera
© Fototeca.cat
Matemàtiques
Corba oberta, intersecció d’un con de revolució amb un pla que forma amb ’eix d’aquell un angle més petit que amb la generatriu.
Constitueix el lloc geomètric dels punts del pla tals que la diferència de llurs distàncies a dos punts fixos, anomenats focus , és una constant, simbolitzada habitualment per 2 a Té dos eixos de simetria i, referida a ells, la seva equació és x 2 / a 2 - y 2 / b 2 = 1, on i 2c és la distància entre els focus L’excentricitat e és c / a Les asímptotes són les rectes y = b / a x asímptota Quan a = b , la hipèrbola és anomenada equilàtera , i la seva equació referida a les asímptotes, que són perpendiculars, és y = k/ x la seva excentricitat és
Johann Christian Doppler
Física
Matemàtiques
Físic i matemàtic austríac.
Fou professor de física i de matemàtiques a les escoles tècniques de Praga i de Chemnitz i professor de física experimental a la Universitat de Viena 1850 El seu treball Über das farbige Licht der Doppelsterne ‘Sobre la coloració de la llum dels estels dobles’, 1842 inclou el fonament teòric de l’efecte que duu el seu nom El 1848 descobrí l’efecte de pertorbació que en les ones sonores i de llum produeix la rotació del medi de propagació Establí, també, un mètode per a determinar la distància i el diàmetre absolut dels estels fixos
el·lipse
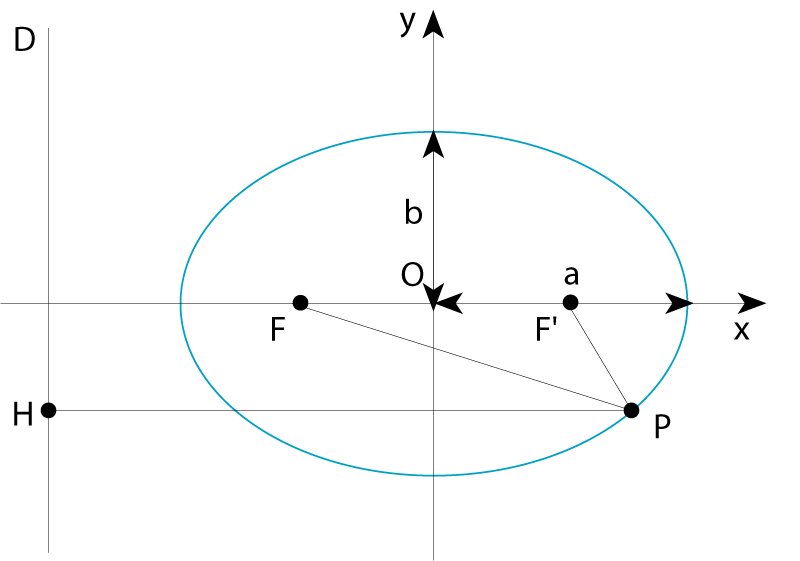
El·lipse de semieixos a i b; D és la directriu associada al focus F
© Fototeca.cat
Matemàtiques
Corba tancada que resulta de la intersecció d’una superfície cònica amb un pla que no és paral·lel a cap generatriu ni a l’eix d’aquella; és doncs, una cònica
.
La seva equació en coordenades cartesianes referides als seus dos eixos perpendiculars de simetria és x 2 / a 2 + y 2 / b 2 =1, a essent el semieix major i b el semieix menor L’ellipse és el lloc geomètric dels punts P del pla tals que la suma de llurs distàncies a dos punts fixos F i F ´, anomenats focus , és una quantitat constant, independent del punt P concret, igual al doble del semieix major, PF + PF ´=2 a és també el lloc geomètric dels punts P tals que el quocient de llurs distàncies a un punt fix, un dels focus, i a…
determinant
Matemàtiques
Donada una matriu quadrada d’ordre
n, A=(a i j
)
, suma dels n
! termes
.
Aquestes termes corresponen a les diferents maneres de fer el producte de n elements de A de manera que n'hi hagui un, i només un, de cada fila i de cada columna Els n termes s’obtenen en fer totes les permutacions dels n subíndexs de columna 1,n mantenint fixos els índexs de fila el nombre r del terme és la signatura de la permutació k 1 k n El determinant de A acostuma a ésser representat tancant la matriu amb dues barres verticals El nombre n és l' ordre del determinant Un determinant pot ésser representat en termes dels elements i cofactors cofactor de qualsevol fila o…
cercle d’Apol·loni
Matemàtiques
Lloc geomètric dels punts del pla tals que la raó de les distàncies a dos punts fixos és constant.
bipolar
Matemàtiques
Dit de les coordenades d’un punt d’un pla definides en donar les seves distàncies a dos punts fixos anomenats pols.
cos
Matemàtiques
Conjunt dotat de dues operacions, que hom acostuma a designar + i × (suma i producte), amb les següents propietats: respecte a la suma el conjunt té estructura de grup commutatiu, i també amb el producte és grup, commutatiu o no, i segons això el cos es dirà d’una manera o d’una altra.
A més, hom exigeix que l’operació × tingui la propietat distributiva respecte a la + Hom pot dir, doncs, que un cos és un anell tal, que cada element té invers respecte a l’operació × Un cos té només dos ideals el 0 i ell mateix Els exemples més immediats són el cos ℝdels nombres reals, amb les operacions usuals de suma i producte, el cos ℚdels nombres racionals i el ℂdels complexos Hi ha el cos de dos elements 0 i 1, amb les operacions + 0 element neutre 1 + 1 = 0, i × habitual Com a exemple de cos no commutatiu hi ha el dels quaternions La característica d’un cos és el nombre més petit p…