Resultats de la cerca
Es mostren 7 resultats
astroide
Astroide
Fototeca.cat
Matemàtiques
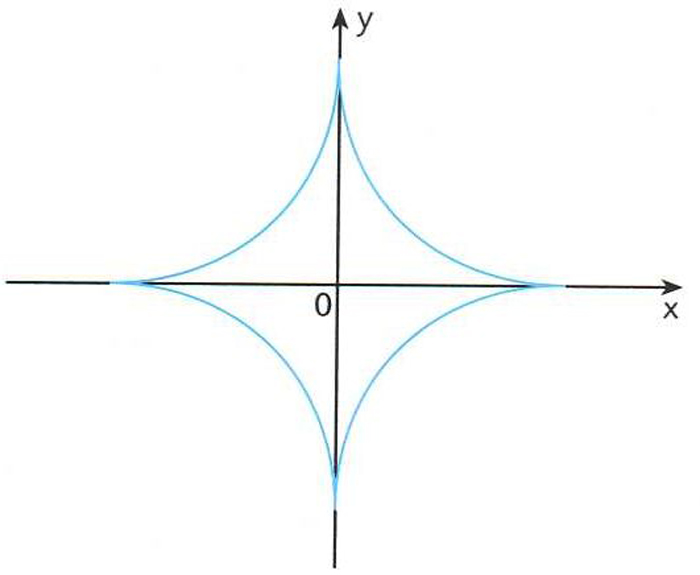
Corba plana algebraica d’equació cartesiana x2/3 + y2/3 = r2/3.
L’astroide és una hipocicloide amb quatre puntes que es genera quan la circumferència que gira té un radi r que val la quarta part del de la circumferència a l’interior de la qual gira
sòlid de revolució
sòlid de revolució
Matemàtiques
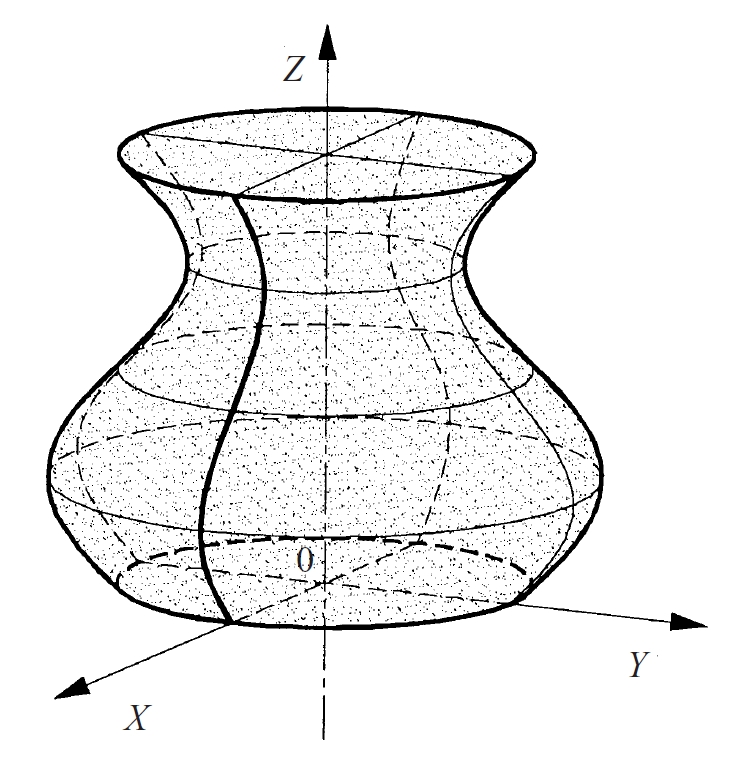
Cos limitat per una superfície de revolució, que hom obté per la rotació d’una línia entorn d’un eix.
Així, l’esfera és el sòlid engendrat per un cercle que gira entorn d’un diàmetre el con de revolució és engendrat per una recta o un segment que talla l’eix al voltant del qual gira
teoremes de Guldin
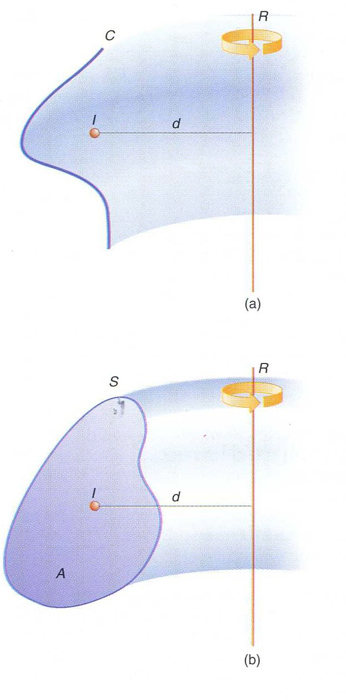
teoremes de Guldin: (a) primer teorema; (b) segon teorema
© fototeca.cat
Matemàtiques
Teoremes que relacionen el centre de massa d’una corba o d’una superfície amb l’àrea o el volum, respectivament, que generen en girar al voltant d’un eix.
Segons el primer teorema de Guldin , donada una corba plana C , de longitud l , que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2π dl , on d és la distància des del centre de massa I de la corba a la recta R en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material El segon teorema de Guldin afirma que, donada una superfície plana S , d’àrea A , que gira al…
paraboloide de revolució
Matemàtiques
Paraboloide que és generat per una paràbola que gira entorn del seu eix de simetria.
Si p és el paràmetre de la paràbola i l’eix de rotació és l’eix OZ, l’equació és x 2 /p + y 2 /p = 2 z
catenoide
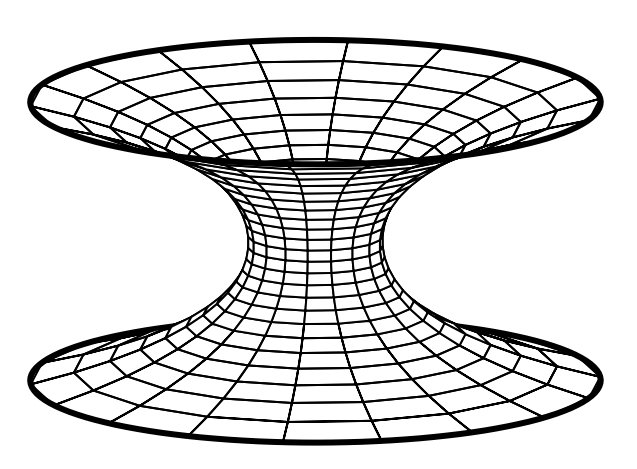
catenoide
Matemàtiques
Superfície mínima de revolució generada per una catenària que gira al voltant de l’eix d’abscisses.
con
Matemàtiques
Superfície reglada generada per totes les rectes (generatrius) que passen per un punt dit vèrtex i per una corba (exterior al punt donat) dita directriu.
La superfície consta de dos fulls units pel vèrtex Es parla de con de revolució si la superfície cònica és engendrada per una recta que passa pel vèrtex i gira al voltant d’una altra recta que també hi passa, la qual és anomenada eix del con Les corbes obtingudes en tallar un con de revolució amb un pla que no passa pel vèrtex reben el nom de seccions còniques o, simplement, còniques Si el pla secant és parallel a una generatriu del con, la cònica rep el nom de paràbola en la resta de casos, el pla secant determina una ellipse o una hipèrbola, segons si el pla talla un full del con o tots…
espiral
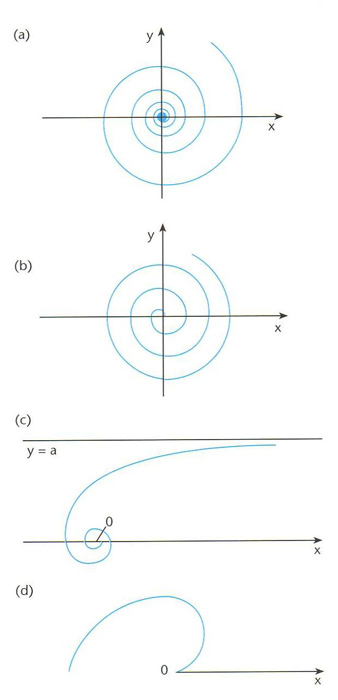
espiral: (a) logarítmica; (b) d’Arquímedes; (c) hiperbòlica; (d) parabòlica
© fototeca.cat
Matemàtiques
Corba plana descrita per un punt que gira al voltant d’un punt fix allunyant-se contínuament segons una llei determinada, característica per a cada tipus d’espiral.
Analíticament són representades gairebé sempre en coordenades polars Les equacions de les espirals més importants són espiral logarítmica o equiangular, r = e aθ espiral d’Arquimedes , r = r o /2πθ espiral hiperbòlica, r θ = a /θ espiral parabòlica o de Fermat, r 2 = a θ, i espiral sinusoidal, r n = a n sin n θ