Resultats de la cerca
Es mostren 12 resultats
espai mètric
Matemàtiques
Espai topològic que té la topologia definida per mitjà d’una distància.
El teorema de metrització d’Urysohn afirma que tot espai normal amb una base de vectors numerables és un espai mètric
successió de Cauchy
Matemàtiques
Successió {Xn} en que la distància entre dos termes, d(xm,xn)>, tendeix a zero quan m,n tendeixen a infinit.
El seu significat és donat un nombre qualsevol ε> 0, existeix un N tal que dx m ,x n > ε quan m,n > N Cal fer notar que tota successió convergent és successió de Cauchy, tenint en compte, tanmateix, que no tota successió de Cauchy és convergent en l’espai mètric de tots els nombres reals, en el qual d α,β = α-β, tota successió de Cauchy és convergent Aquest és un exemple d’un tipus important d’espais mètrics l’espai mètric complet , definit com un espai mètric en el qual tota successió de Cauchy és convergent
Louis François Antoine Arbogast
Matemàtiques
Matemàtic francès.
Fou el responsable de l’adopció del sistema mètric decimal a la República Francesa Les seves idees matemàtiques prefiguren l’obra de Cauchy, Boole, Hamilton i Grassmann
distància
Matemàtiques
Donat un conjunt E
, aplicació d
: Ex
E →ℝ +
que satisfà els següents axiomes:
o sia, la distància és estrictament positiva, simètrica i compleix la desigualtat triangular.
Tot conjunt E en el qual hi ha definida una distància d és un espai mètric , i d és la mètrica de l’espai Per exemple, en el conjunt dels números reals ℝhom pot considerar d x,y = | x — y |, valor absolut de la diferència x — y , on x,y ∈ℝ
uniformitat
Matemàtiques
Família F de subconjunts d’un producte cartesià T × T
.
Compleix x,x pertany a qualsevol element de F , per a tot x si V és de F, V - 1 = { x,y | y,x és de V} és també de F i per a tot V de F existeix un altre W tal que WW = { x,z | existeix y en T i x,y ∈ W , y,z ∈ W} és un subconjunt de V Tota uniformitat dóna lloc a un espai topològic i aquest és metritzable la seva topologia prové d’una distància si és de Hausdorff i la uniformitat té una base numerable Per exemple, si T és un espai mètric, amb distància d , el conjunt de subconjunts de T × T , U ∈ = { x,y | d x,y πε} és una uniformitat La parella T,F , on T és…
moviment
Matemàtiques
Aplicació d’un espai mètric en ell mateix que conserva la distància.
Actualment hom tendeix a anomenar-lo isometria El conjunt de moviments definits sobre un espai, amb l’operació de composició o producte de moviments, constitueix un grup En particular, és interessant l’estudi dels moviments al pla i a l’espai ordinaris El grup dels moviments del pla és generat per les simetries axials, és a dir, tot moviment del pla pot ésser descompost en producte d’un cert nombre de simetries axials Els de nombre parell són anomenats moviments directes , conserven el sentit del pla i són un subgrup del grup de moviments els altres són anomenats moviments inversos Dins el…
isometria
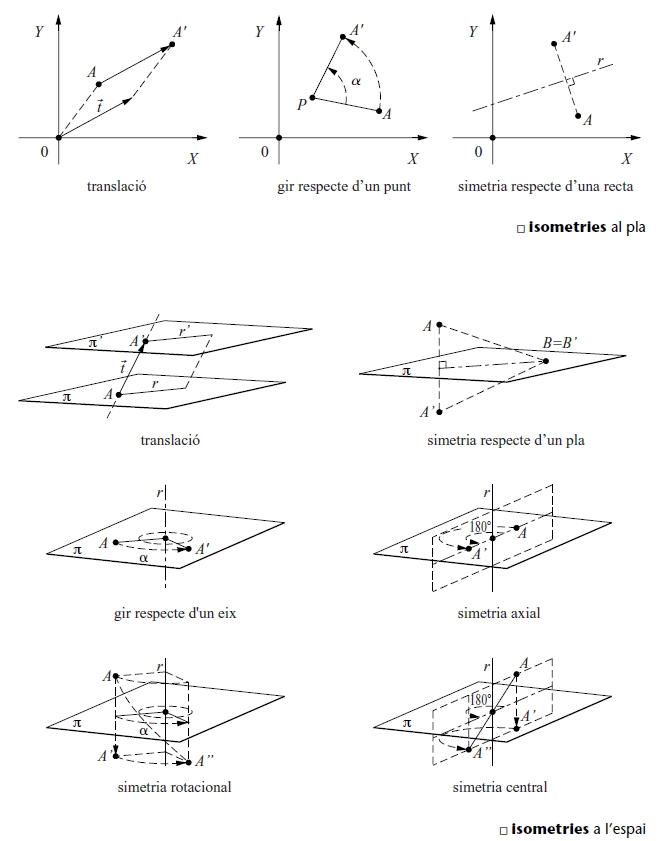
isometria
Fototeca.cat
Matemàtiques
Aplicació d’un espai mètric en ell mateix que conserva la distància.
Les isometries més conegudes són les translacions, les rotacions i les simetries del pla o de l’espai ordinaris
Carlos Ibáñez e Ibáñez de Ibero

Carlos Ibáñez e Ibáñez de Ibero
© Fototeca.cat
Història
Militar
Matemàtiques
Matemàtic i militar.
El 1839 ingressà a l’acadèmia d’enginyers de l’exèrcit Publicà, amb Joan Modet, un Manual del pontonero 1853 Aquell mateix any fou membre de la comissió que havia de fer el mapa de l’Estat espanyol i inicià, així, els seus notables treballs geodèsics Feu construir, sota la seva direcció, a París, un aparell per a mesurar bases geodèsiques, que fou consultat pel govern egipci fou elegit membre de l’Institut Egipci Fou nomenat cap del primer districte geodèsic cadastral, que comprenia aleshores el País Valencià i les Illes Balears El 1864 publicà Estudio sobre la nivelación geodésica , i el…
esfera
Matemàtiques
En un espai mètric de distància d, conjunt de punts x la distància dels quals a un cert punt fix p és igual a un nombre real positiu r.
El centre de l’esfera és p i el radi r , i es denota per S p r A ℝ n l’esfera de centre 0 i radi 1 es denota per S n –1 i rep el nom d’ esfera unitat
relació de proximitat
Matemàtiques
Relació binària S entre els subconjunts d’un conjunt E, que fou introduïda per Efremovič per tal de generalitzar la relació ‘‘ésser pròxim’’ que hom utilitza correntment en l’espai mètric ordinari.
La relació de proximitat és definida pels axiomes següents ASB ⇔ BSA , és a dir, la relació S és simètrica ASB ⇒ A ≠∅i B ≠∅, és a dir, el conjunt buit no és pròxim a cap altre AS B ∪C ⇒ ASB o ASC , és a dir, un conjunt és pròxim a la reunió de dos conjunts si és pròxim, almenys, a un d’ells A ∩B ≠∅⇒ASB , és a dir, dos conjunts que es tallen són pròxims { X } S { Y } ⇔ X=Y , és a dir, un punt només és pròxim a si mateix si A$B aleshores existeix un conjunt C tal que B$C i A$C c , on C c és el conjunt complementari de C Tota proximitat indueix una topologia prenent com a conjunts tancats els…