Resultats de la cerca
Es mostren 129 resultats
trisecció d’un angle

Trisecció d’un angle, mitjançant la "destral índia"
Matemàtiques
Divisió d’un angle en tres angles iguals.
La trisecció d’un angle constituí un dels problemes clàssics, i hom demostrà que és insoluble gràficament mitjançant el regle i el compàs per a la solució cal emprar corbes d’ordre superior al segon, com la concoide de Nicomedes
anàlisi de Fourier
Física
Matemàtiques
Estudi de les funcions que té per finalitat d’expressar-les mitjançant una sèrie o una integral en què intervenen les funcions trigonomètriques.
El fonament d’aquesta tècnica matemàtica és l’anomenat, de vegades, teorema de Fourier Tota funció periòdica f x , contínua o, com a màxim, amb un nombre finit de discontinuïtats finites, pot expressar-se mitjançant una sèrie trigonomètrica, de la següent manera la sèrie que apareix en aquesta expressió és la sèrie de Fourier de o associada a la funció f x El nombre ω és la pulsació fonamental de la sèrie de Fourier de f i és igual a la pulsació o freqüència angular de f , és a dir, ω=2π/ T , on T és el període de f El primer terme de la sèrie de Fourier de f , terme que…
demostració
Lògica
Matemàtiques
Derivació d’un enunciat, mitjançant l’aplicació d’unes determinades regles lògiques, a partir d’uns altres enunciats, dits premisses de la demostració.
Qualsevol cadena de demostracions ha d’arrencar d’un conjunt finit de premisses no demostrables, els axiomes Aquest conjunt és anomenat el sistema dels axiomes de la teoria deductiva, i els enunciats que són demostrats a partir dels axiomes s’anomenen teoremes Identificada, en la teoria platònica, amb la definició, Aristòtil la considerà com un procés superior, adreçat a extreure, mitjançant el sillogisme, una conclusió a partir d’unes premisses certes L’escolàstica s’adherí a l’esquema aristotèlic i n'elaborà una classificació propter quid , ad intellectum , ad sensum , a priori , a…
base d’un espai vectorial
Matemàtiques
Conjunt de vectors linealment independents que generen l’espai vectorial mitjançant combinacions lineals, és a dir, tals que qualsevol vector v de l’espai pot ésser expressat d’una manera unívoca com a combinació lineal dels vectors de la base:
Les coordenades a 1 ,, a n de v en la base e 1 ,, e n són úniques Tot espai vectorial té una base és una conseqüència de l’axioma de Zermelo Si l’espai E té una base formada per un nombre finit d’elements base finita l’espai és de dimensió finita aleshores totes les bases tenen el mateix nombre d’elements, nombre que s’anomena la dimensió de l’espai , dim E Un espai vectorial de dimensió finita té infinites bases Dues bases de E , B = e 1 ,, e n i B’ = e’ 1 ,, e’ n es relacionen mitjançant una matriu de canvi de base essent és a dir, les matrius A i B són inverses B = A…
potència
Matemàtiques
Donats un nombre a
, anomenat base
, i un nombre natural n
, anomenat exponent
, producte
a n
de n
factors iguals a a
, és a dir,
.
Hom generalitza la noció de potència al cas en què l’exponent és un enter negatiu, mitjançant la fórmula a -n =1/a n , i al cas en què l’exponent és un nombre racional, mitjançant la fórmula La generalització al cas que l’exponent sigui un nombre real qualsevol té lloc mitjançant la funció exponencial , i en el cas que l’exponent sigui un nombre complex, mitjançant la fórmula de De Moivre Les propietats més importants de les potències són
integrador
Electrònica i informàtica
Matemàtiques
Tecnologia
Aparell o dispositiu, mecànic o electrònic, destinat al càlcul d’integrals.
Els mecànics poden ésser intègrafs intègraf o integròmetres integròmetre Els integradors electrònics poden efectuar la integració directament sobre un senyal analògic mitjançant amplificadors operacionals, bé que pel mostreig d’un senyal digital i el seu processament mitjançant circuits integrats o bé mitjançant un programa que calculi la funció integral
derivació sota el signe integral
Matemàtiques
Derivació d’una funció expressada mitjançant una expressió integral.
Així, si fx = ∫ b a F x,y dy, aleshores la seva derivada és donada per l’expressió integral f'x = ∫ b a ∂F x,y /∂ x dy Aquesta forma d’obtenir la derivada és anomenada regla de Leibniz
sistema de coordenades
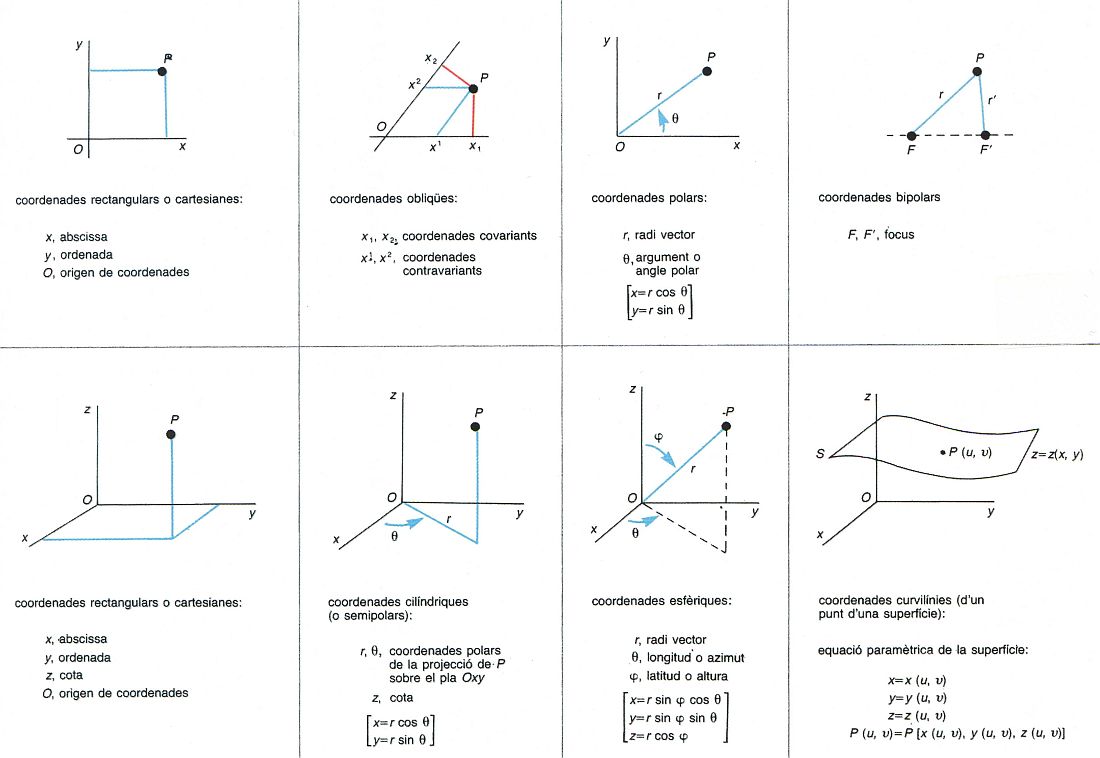
Sistemes de coordenades matemàtiques: coordenades d’un punt del pla (superior) i d’un punt de l’espai (inferior)
©
Matemàtiques
En un cert domini X, conjunt de funcions tal, que els valors en un punt el determinen, de manera que mitjançant un sistema de coordenades cada punt és definit per un conjunt de nombres, que són les coordenades del punt.
Segons els casos les funcions d’un sistema han de complir certes condicions Així, en el pla, un sistema de coordenades lineal consisteix en dues funcions lineals independents Els eixos del sistema són les rectes que corresponen al valor zero de cadascuna de les funcions La intersecció dels dos eixos és l' origen de coordenades Si els eixos són perpendiculars, el sistema és rectangular i les coordenades són rectangulars o cartesianes Si els eixos són oblics, les coordenades són obliqües o rectilínies obliqües En aquest cas, hom pot considerar les coordenades covariants o contravariants , que…
inclusió estricta
Matemàtiques
Relació d’ordre estricte entre conjunts.
Es nota mitjançant el símbol ℮ o mitjançant ⊂ si hom empra el símbol ⊆ per a la inclusió no estricta, definida per la condició A ℮ B o, respectivament A ⊂ B si i només si tots els elements de A pertanyen a B però A no és igual a B és a dir B té elements altres que els de A En aquest cas, hom diu que el conjunt A és inclòs estrictament en el conjunt B o que A és un subconjunt estricte de B
operador
Física
Matemàtiques
Aplicació entre dos conjunts de funcions.
Si l’aplicació és lineal, l’operador és anomenat lineal En general hom aplica els qualificatius de les funcions als operadors Així, operador invers té el mateix sentit que aplicació entre funcions inversa Els operadors més importants són els obtinguts mitjançant combinacions de derivades operadors diferencials , o mitjançant combinacions d’integrals operadors integrals En mecànica quàntica, hom associa un operador a cada magnitud física o observable Aquest operador, en actuar sobre la funció d’ona que representa l’estat d’un sistema quàntic, permet de calcular…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina