Resultats de la cerca
Es mostren 14 resultats
ordre d’una derivada
Matemàtiques
Respecte a una funció original, f, nombre de derivacions que hom ha fet fins a arribar a la derivada en qüestió.
Si f n és la derivada d’ordre n , o derivada n-èsima , de la funció f , se satisfà que f n = f n-1 '
resolvent
Matemàtiques
Donada una equació de quart grau amb solucions x1, x2, x3, x4 , equació de tercer grau que té com a solucions (x1+x2 ) · (x3+x4 ), (x1+x3 )·(x2+x4 ) i (x1+x4 )·(x2+x3 ).
Si l’equació de quart grau és de la forma x 4 +px 2 +qx+r = 0 la seva resolvent és y 3 -2py 2 + p 2 -4r y + q 2 = 0 A partir de les solucions d’aquesta equació cúbica hom n'obté fàcilment les de l’equació original
ordre d’una derivada parcial
Matemàtiques
Respecte a una funció original, f, nombre de derivacions parcials que hom ha fet fins a arribar a la derivada en qüestió.
Per exemple, les derivades parcials de ∂ f /∂ x i són les derivades parcials d’ordre 2 , o de segon ordre , de f , i són notades per ∂ 2 f /∂ x j ∂ x i on j = 1, , n
Aristeu de Crotona
Matemàtiques
Matemàtic grec.
Escriví cinc llibres sobre Els llocs sòlids on formulà teoremes sobre els cinc sòlids regulars i sobre les corbes còniques Influí sobre Euclides, bé que el tractat d’Aristeu és més important i original Les seves obres només són conegudes per referències de Pappus i Euclides Això fa que tota l’originalitat de l’estudi de les còniques recaigui sobre Apolloni de Perge
Nikolaj Ivanovič Lobačevskij
Matemàtiques
Matemàtic rus.
En el seu llibre Algebra ili isčislenie konečnykh ‘Àlgebra, o càlcul de finits’, 1834 presentà un mètode original per a calcular arrels complexes El 1835 publicà Novyje Načala geometrij s polnoj teorija paralllelnykh ‘Nous principis de la geometria amb una teoria completa de parallels’, on, en negar la possibilitat del cinquè postulat d’Euclides, donà lloc a una geometria no euclidiana, els detalla i les aplicacions de la qual exposà en Pangeometrija 1855
Julius Plücker
Física
Matemàtiques
Matemàtic i físic alemany.
Fou professor a les universitats de Berlín, Halle i Bonn Féu recerques, juntament amb Hittorf, sobre els gasos enrarits 1865, l’òptica dels cristalls i els espectres de gasos Estudià i analitzà els raigs catòdics i llur desviació pels camps magnètics 1868 És conegut sobretot pels seus treballs en geometria analítica, on introduí una noció original de coordenades coordenades plückerianes Publicà, entre altres obres, Analytisch-geometrische Entwicklungen 1835, Theorie der algebraischen Kurven 1839 i Neue Geometrie des Raumes 1868
Leví ben Geršom
Astronomia
Filosofia
Matemàtiques
Metge, matemàtic, astrònom, filòsof i exegeta.
Tingut per heterodox, fou el pensador més original del judaisme medieval, després de Maimònides Escriví cinc llibres de matemàtiques i un de lògica i fou un dels primers a escriure sobre trigonometria plana En astronomia enginyà nous aparells, als quals dedicà un poema Comentarista del Pentateuc i d’una dotzena més de llibres bíblics, de la Isagoge de Porfiri i d’obres d’Aristòtil, a la seva obra principal, Milḥamot Adonay ‘Les guerres del Senyor’, sobre la filosofia de la religió, s’inclina vers l’aristotelisme
integral primera
Matemàtiques
En una equació diferencial ordinària de segon ordre, equació diferencial ordinària de primer ordre, que resulta de fer una integració en l’equació original.
Així, per exemple, l’equació de la conservació de l’energia mecànica és obtinguda en fer una integració de l’equació del moviment d’un sistema conservatiu hom diu que l’energia és una integral primera del moviment, o, simplement, una integral del moviment
aplicació
fototeca.cat
©
Matemàtiques
correspondència
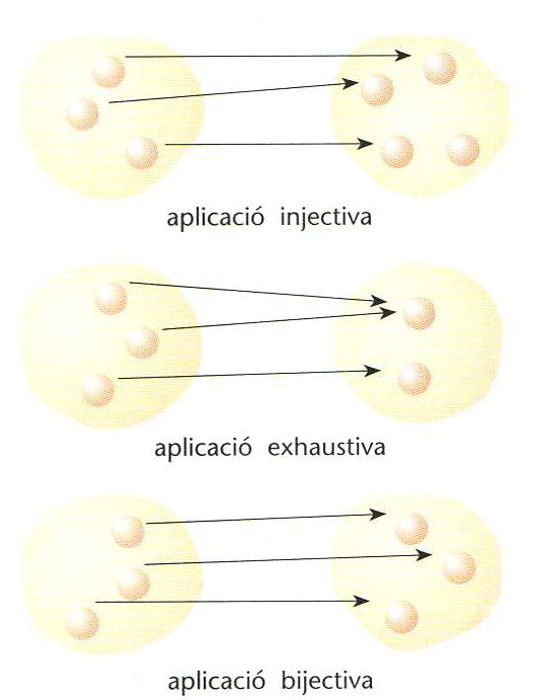
entre dos conjunts en què tot element del primer conjunt (o original) té una imatge i una de sola en el segon conjunt.
Si elements diferents tenen imatges diferents, l’aplicació és dita injectiva si tot element del segon conjunt és imatge d’un element almenys del primer, l’aplicació és exhaustiva una aplicació que sigui alhora injectiva i exhaustiva és dita bijectiva o unívoca
divisibilitat
Matemàtiques
Conjunt de condicions que han de complir dos nombres enters per tal que hom pugui efectuar la divisió exacta de l’un per l’altre, o sia, que compleixin la condició a = bc, a essent el múltiple, b, el divisor, i c, el quocient exacte.
Per efectuar aquest estudi hom parteix de la descomposició en factors primers a ℤ Les proves de divisibilitat permeten de saber si un nombre és divisible per un altre sense necessitat de fer-ne la divisió En són exemples els següents tot nombre acabat en un dígit parell és divisible per 2 tot nombre acabat en 0 o 5 és divisible per 5 tot nombre tal que la suma dels seus dígits és 3 o 9 és divisible, respectivament, per 3 o 9 si els dos darrers dígits d’un nombre formen un nombre divisible per 4, el nombre original també ho és i qualsevol nombre la suma dels dígits del qual és…