Resultats de la cerca
Es mostren 150 resultats
delta de Dirac
Matemàtiques
Funció simbòlica δ(x) que permet de representar formalment les transformacions funcionals idèntiques com a transformacions integrals.
L’ús formal de δ x forneix una notació que permet la generalització de moltes relacions matemàtiques Per a una variable real x , és definida per les condicions de tal forma, que per a qualsevol x sempre satisfà Proposada per Dirac el 1930 com a preocediment heurístic, fou establerta rigorosament per Laurent Schwartz
digraf de De Brujin
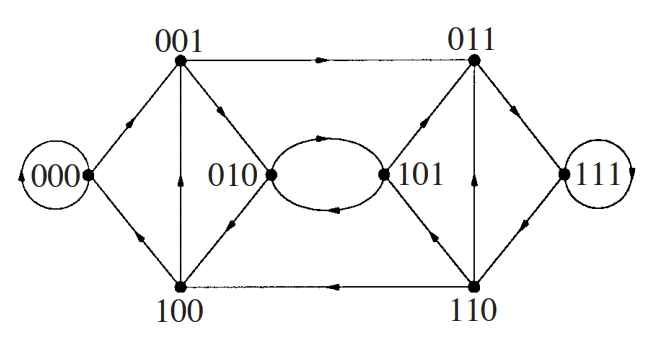
digraf de De Brujin
Matemàtiques
Digraf B(d,D) que té per conjunt de vèrtexs totes les paraules de longitud D que es poden formar amb els d símbols diferents d’un alfabet i tal que una paraula és adjacent respecte a una altra si la primera sense el símbol inicial és igual a la segona sense el símbol final.
El digraf deDe Bruijn és un digraf eulerià, d -regular, que té d elevat a D + 1 arcs Els digrafs deDe Bruijn són útils en el disseny de grans xarxes d’interconnexió
axioma de l’elecció
Matemàtiques
Axioma que admet que, donat un conjunt A, existeix una aplicació f del conjunt dels subconjunts no buits de A en A tal que f(B) pertany a B per a tot B de A diferent del buit.
D’una manera informal, l’aplicació f escull un element de cada subconjunt no buit de A Cal fer notar que no és un axioma constructiu, en el sentit que no es té cap indicació sobre la manera de construir una tal f L’axioma de l’elecció equival a la possibilitat de dotar qualsevol conjunt d’una bona ordenació teorema de la bona ordenació L’axioma de l’elecció és equivalent al lema de Zorn
gràfic de control
Matemàtiques
Representació cronològica d’observacions relatives a mostres tretes d’un procés industrial per tal de controlar les característiques del producte i corregir, si cal, el funcionament del procés.
En el gràfic de control hom representa, generalment, les mitjanes i les amplituds diferència entre el valor més gran i el més petit de la mostra de les mostres El sistema de referència és constituït per uns eixos de coordenades i unes rectes horitzontals o límits que indiquen la necessitat d’extreure una mostra complementària límit d’atenció o bé d’intervenir directament en el procés pertalde corregir-lo límit d’intervenció
relació de proximitat
Matemàtiques
Relació binària S entre els subconjunts d’un conjunt E, que fou introduïda per Efremovič per tal de generalitzar la relació ‘‘ésser pròxim’’ que hom utilitza correntment en l’espai mètric ordinari.
La relació de proximitat és definida pels axiomes següents ASB ⇔ BSA , és a dir, la relació S és simètrica ASB ⇒ A ≠∅i B ≠∅, és a dir, el conjunt buit no és pròxim a cap altre AS B ∪C ⇒ ASB o ASC , és a dir, un conjunt és pròxim a la reunió de dos conjunts si és pròxim, almenys, a un d’ells A ∩B ≠∅⇒ASB , és a dir, dos conjunts que es tallen són pròxims { X } S { Y } ⇔ X=Y , és a dir, un punt només és pròxim a si mateix si A$B aleshores existeix un conjunt C tal que B$C i A$C c , on C c és el conjunt complementari de C Tota proximitat…
nombres de Fermat
Matemàtiques
Nombres, Fn, definits per l’expressió (per a n = 1,2,3,...).
El 1640 Fermat cregué que aquests nombres eren primers, però l’any 1740 Euler donà una descomposició per a F 5 = 4 294 967 297, com a producte de 641 per 6 700 417, i posteriorment hom ha demostrat que per a n tal que 5 ≤n≤17 , F n no és primer, i que d’altres nombres de Fermat, com F 1 9 4 5 , F 3 3 1 0 i F 6 5 3 7 són descomponibles El 1796 Gauss demostrà que els únics polígons regulars que hom pot construir amb regle i compàs són els que tenen un nombre de Fermat de costats
fórmula de Tartaglia
Matemàtiques
Fórmula que dóna la solució de l’equació de tercer grau ax3+bx2+cx+d = 0 per coeficients a, b, c i d reals.
La substitució de la incògnita x per la incògnita auxiliar y tal, que x = y-b /3 a converteix l’equació en una del tipus y 3 + py + q =0 les arrels de la qual són obtingudes per la fórmula de Tartaglia, anomenada també fórmula de Cardano , a partir dels nous paràmetres p i q
sèrie de funcions
Matemàtiques
Successió de funcions {
F n
} amb
, on les
f i
són també funcions.
Hom la indica per Σ f n Si { F n } té per límit una funció f , hom diu que la sèrie Σ f n és convergent cap a la funció f i que f és la seva suma, dins el domini on això tingui sentit Si les f i són funcions potencials, f i x = a i x i , la sèrie Σ f n és anomenada sèrie de potències Si la variable x és complexa hom pot demostrar que hi ha un nombre positiu R tal que per a tot x tal que | x | < R la sèrie numèrica Σ a n x n és absolutament convergent, mentre que per a tot x tal que…
teorema de Bonnet
Matemàtiques
Teorema segons el qual els coeficients de les formes fonamentals d’una superfície determinen localment la parametrització de la superfície, llevat de composició amb transformacions ortogonals pròpies i translacions.
Concretament, si E , F , G , e , f , g són funcions diferenciables definides en un obert V ⊂ ℝ 2 , amb E > 0, G > 0 i EG – F 2 > 0 tals que satisfan les equacions de compatibilitat de Gauss i de Mainardi-Codazzi, aleshores per a cada q ∈ V existeix un entorn U ⊂ V de q i un difeomorfisme x U → x U ⊂ ℝ 3 tal que la superfície regular x U ⊂ ℝ 3 té E , F , G , e , f , g per coeficients en les seves formes fonamentals Amés, si U és connex i x’ U → x’ U ⊂ ℝ 3 és un altre difeomorfisme que…
àlgebra de successos
Matemàtiques
És una família, no buida, A
de parts d’Ω tal que, per a cada A
∈ A
,Ω − A
∈ A
i, per a cada parella, A 1
, A 2
∈ A
, A 1
⋂ A 2
∈ A
.
Cada un dels elements A ∈ A és anomenat un succés de l’àlgebra A A voltes hom considera famílies en les quals, per a cada collecció numerable Són anomenades Ϭ-àlgebres de successos
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina