Resultats de la cerca
Es mostren 15 resultats
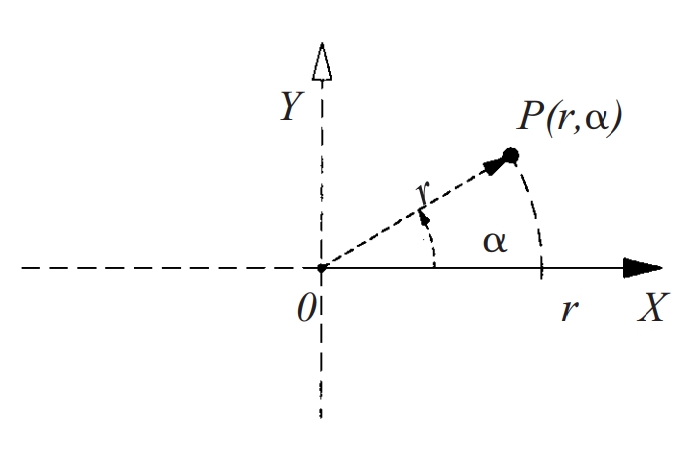
coordenades polars
coordenades cartesianes al pla
Matemàtiques
Parell de nombres (r, α) que permeten localitzar un punt del pla, essent r la distància del punt a un punt fix (pol) i α l’angle que forma la recta que uneix el punt i el pol amb una semirecta fixa que passa pel pol i que és anomenada eix polar.
estrofoide
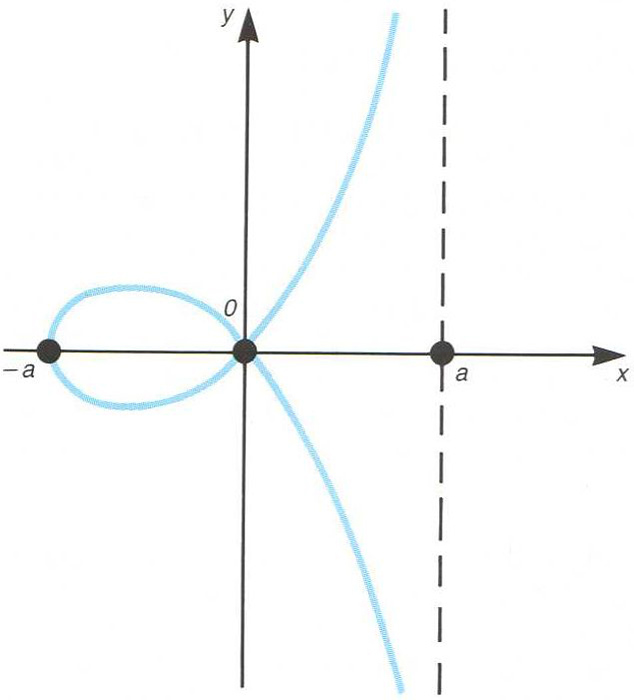
Estrofoide
© fototeca.cat
Matemàtiques
Corba plana, cúbica circular d’equació cartesiana
y 2
( a-x
) =
x 2
( a+x
), a
>0.
L’origen és un punt doble L’equació en coordenades polars és r = - a cos 2ϑ/cos ϑ La línia x = a n'és una asímptota
cardioide
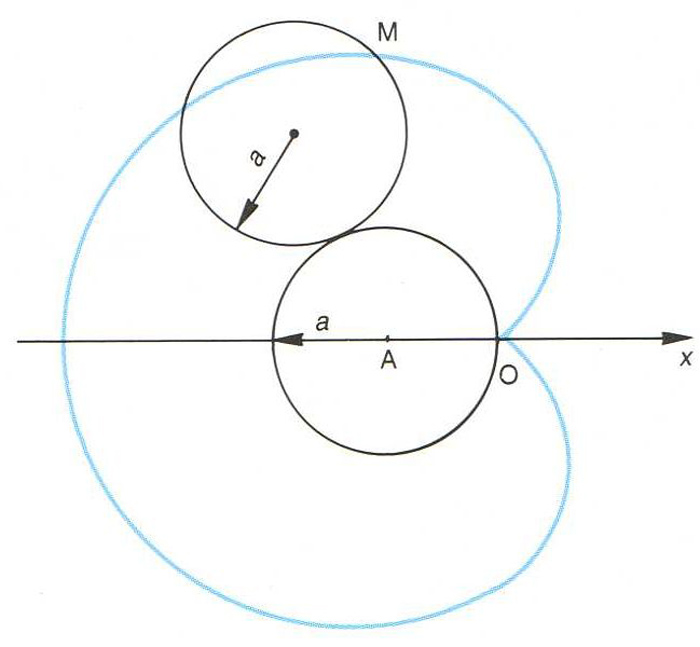
Cardioide determinada pel punt fix M d’un cercle de radi a que roda sense lliscar sobre un cercle fix de radi a i centre A. O és el punt de retrocés
© fototeca.cat
Matemàtiques
Epicicloide singular engendrada per les posicions d’un punt d’un cercle de radi a que roda sense lliscar per damunt d’un altre cercle del mateix radi.
Té un punt de retrocés O , respecte al qual l’equació de la cardioide en coordenades polars és ρ = 2 a 1-cos θ La longitud de la cardioide és aleshores 16 a i l’àrea és 6π a 2
element de superfície
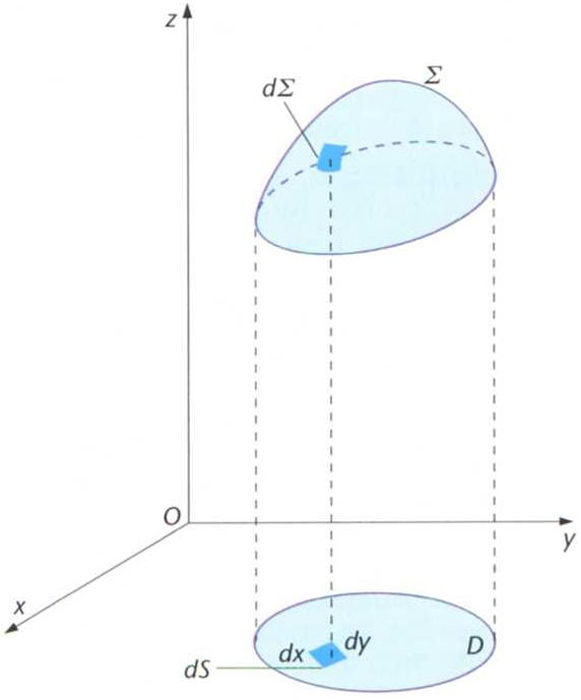
Element de superfície
© fototeca.cat
Matemàtiques
Cadascuna de les parts infinitesimals en què hom divideix una superfície a l’hora de calcular-ne l’àrea.
En coordenades cartesianes l’element de superfície dS val dS = dx dy , i en coordenades polars dS = ρ d ρ d θ L’àrea A d’una superfície regular z = f x,y que tingui com a projecció en el pla XOY un recinte S , és igual a la integral doble expressada per
espiral
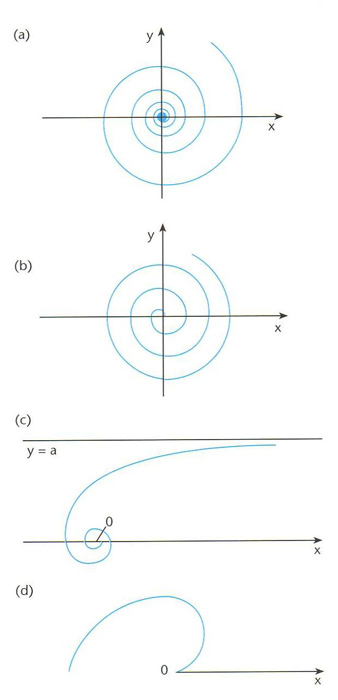
espiral: (a) logarítmica; (b) d’Arquímedes; (c) hiperbòlica; (d) parabòlica
© fototeca.cat
Matemàtiques
Corba plana descrita per un punt que gira al voltant d’un punt fix allunyant-se contínuament segons una llei determinada, característica per a cada tipus d’espiral.
Analíticament són representades gairebé sempre en coordenades polars Les equacions de les espirals més importants són espiral logarítmica o equiangular, r = e aθ espiral d’Arquimedes , r = r o /2πθ espiral hiperbòlica, r θ = a /θ espiral parabòlica o de Fermat, r 2 = a θ, i espiral sinusoidal, r n = a n sin n θ
pla complex
Matemàtiques
Pla de ℝ 2
obtingut mitjançant la identificació dels punts < x
, y
> amb els nombres complexos x
+ iy
.
Aquest pla rep també el nom de pla de Gauss o de Gauss-Argand Un punt z = < x , y > admet una representació en coordenades polars i, per tant, z = ρ ⋅ cos θ + i ⋅ sin θ que, d’acord amb la identitat d’Euler, hom escriu z = ρ ⋅ e i⋅θ Aquesta expressió permet de calcular amb facilitat les potències dels nombres complexos i extreure'n les seves arrels n -èsimes Resulta aleshores que la fórmula de Moivre s’expressa
quàdrica

Matemàtiques
Dit de la superfície algèbrica de segon grau les coordenades (x, y, z) dels punts de la qual satisfan una equació del tipus la qual hom acostuma a escriure, fent servir notació matricial, .
Si notem la primera matriu associada a les coordenades d’un punt per α, i la segona formada pels coeficients de la quàdrica per β, aleshores l’anterior expressió pot escriure's com α t βα ═ 0, on α t és la matriu transposada de α Dos punts M 0 i M 1 són dits conjugats respecte a una quàdrica quan llurs matrius satisfan α t 0 βα 1 = 0 Un pla és anomenat pla polar d’un punt respecte a una quàdrica quan és format pels punts conjugats del punt considerat Hom anomena centre de la quàdrica qualsevol punt conjugat de tots els punts de l’infinit, i plans diametrals , els plans polars…
concoide d’una corba respecte a un punt
Matemàtiques
Donada una corba C
i un punt O
del seu pla, lloc geomètric dels punts Q
i Q’
determinats en mesurar, a ambdós costats, una determinada distància b
a partir del punt P
obtingut en tallar la corba C
mitjançant una recta R
que passi per O
.
De la definició resulta palès que la concoide d’una corba té dues branques Si C és una recta, i hom escull un sistema de coordenades polars amb origen al punt O , separat de C per una distància perpendicular a , l’expressió de la concoide de la recta C respecte a O és r= a/cos θ+ b si a < b es determina un llaç en O , si a = b hi ha una cúspide en O i la concoide és la concoide de Nicomedes , i si a > b no hi ha cúspide però hi ha un acnode en O Un altre cas particular s’escau quan C és una circumferència en aquest cas, la concoide de la circumferència C respecte a un…
Johann Bernoulli
Matemàtiques
Matemàtic suís.
Començà estudiant medicina, però es decantà molt aviat per les matemàtiques Fou deixeble del seu germà Jakob, que l’inicià en l’obra de Leibniz, de la qual fou propagador Estigué a París 1690-95, on redactà un curs de càlcul per al marquès de L’Hôpital hom creu que la coneguda regla de L’Hôpital és deguda a Johann Bernoulli El 1691 determinà les tangents i els radis de curvatura de moltes corbes planes i donà el primer exemple de coordenades polars Fou professor a Groningen 1695-1705 i, des de la mort del seu germà Jakob, a Basilea 1705, on fou mestre d’Euler Proposà i resolgué…